How Many Sides Does A Regular Polygon

Introduction

We learn to identify shapes when we are young. We can now identify shapes like triangles, squares, rectangles, etc. These shapes are part of 2-dimensional closed geometric figures known as polygons. Any geometric figure with a finite number of sides is known as a polygon. A polygon's sides are straight lines connecting the vertexes and creating a closed figure. Whenever a polygon has congruent or equal-length sides, it is called a regular polygon.

Sides in A Regular Polygon

A regular polygon has sides with the same length value and their interior angles are also the same. Based on the number of sides each polygon has, they all have different names. Look at the following table to get an idea.

Though we have only made a list of regular polygons with upto 10 sides, this list can continue to as many sides we want. As long the sides are of equal length, and the interior angles are equal, it will be a regular polygon.

As you can see in the above table, we have found the interior angle of each polygon. You can do this too using the following formula

\text{Angle between two adjacent sides}=\Theta =\begin{aligned} &\text{(n-2)} \times \frac {180}{\text n} \end{algined}

Let's use the above equation to solve the following examples

Example 1 - What is the value of interior angle of a regular polygon if it has 4 sides

Above equation can be solved as follows

\begin{aligned}

\Theta& =\text{(n-2)} \times \frac {180}{\text n}\

&=(4-2) \times \frac{180}{4}\

&=2 \times 45\

&=90 \hspace{1mm}\text{degs}

\end{algined}

Example 2 - What is the value of interior angle of a regular polygon with 25 sides?

The above problem can be solved as follows

\begin{aligned}

\Theta&=\text{(n-2)} \times \frac {180}{\text n}\

&=(25-2) \times \frac{180}{25}\

&=23 \times 7.2\

&=165.6 \hspace{2mm}\text{degs}

\end{algined}

Properties af A Regular Polygon

Following are some properties of a regular polygon that we must always keep in mind.

• Sides of a regular polygon are of equal length

• The interior angles between two lines are equal

• The perimeter length of a regular polygon with n sides is equal to the length of one side multiplied by the total number of sides.

• Diagonals in a regular polygon with ‘n’ sides can be found using the below formula

\frac{n(n-3)}{2}

Sum of all interior angles of a regular polygon with ‘n’ sides can be found using the below formula

\begin{aligned}

& \text{(n-2)} \times 180

\end{algined}

Examples

Find the interior angle for a regular polygon with 15 sides.

Solve the above problem as follows

\begin{aligned}

\Theta &=\text{(n-2)} \times \frac {180}{\text n}\

&=(15-2) \times \frac{180}{15}\

&=13 \times 12\

&=156 \hspace{2mm}\text{degs}

\end{algined}

Find the total number of diagonals in a pentagon

As we know, a pentagon has 5 sides to it. We can solve the above problem as follows

\begin{aligned}

&\frac{\text{n(n-3)}}{2}\

&=\frac{5(5-3)}{2}\

&=\frac{5 \times 2}{2}\

&=\frac{10}{2}\

&=5

\end{aligned}

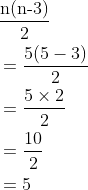
Notes

• A regular polygon can have as many sides above 3, as long as they are of equal length and the interior angles are equal.

• A regular polygon with 10 sides is called a Decagon.

• A rectangle is not considered a regular polygon. Though all the interior angles are equal, the length of the sides differ. Therefore, not a regular polygon.