How Many Rational Numbers Are There Between Two Rational Numbers?

There are infinite rational numbers between any two given rational numbers.

The numbers that may be represented in the form of \frac{p}{q} with q\neq 0 are referred to as rational numbers. Prime and composite numbers, odd and even integers, decimals, and fractions are a few examples of rational numbers. It is possible to find several rational numbers between two rational numbers. We can discover infinite rational numbers between any two rational numbers.

How To Determine The Rational Numbers Between Two Rational Numbers With The Same Denominator Value

• Checking the value of the denominators is the first step in identifying the rational numbers between two rational numbers.

• Check the numerators if the denominator values are the same.

• We should write the rational numbers between the two rational numbers in increments of one for the numerator if the numerators vary by a significant amount without changing the denominator's value.

• The numerators and denominators of both rational numbers are multiplied by multiples of 10 if the values of the numerators differ by a smaller value than the number of rational numbers to be found.

If the denominators are different, we have to equate them using by LCM method.

Let us find the rational numbers between \frac{2}{5} and \frac{11}{5}

We can insert the values \frac{3}{5}, \frac{4}{5}, \frac{5}{5}, \frac{6}{5}, \frac{7}{5}, \frac{8}{5}, \frac{9}{5}, \frac{10}{5}

between \frac{2}{5} and \frac{11}{5} .

Now, we can change the denominator by dividing and multiplying by 10.

\frac{2\times 10}{5\times 10}=\frac{20}{50} \

\frac{11\times 10}{5\times 10}=\frac{110}{50}\

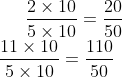
We can insert many numbers as \frac{21}{50} ... till \frac{109}{50} .

This way, we can multiply and divide by 10 again and get many numbers between rational numbers. Therefore, between two rational numbers, there can be infinite rational numbers.

Examples

1. Find the 3 rational numbers between \frac{21}{50} and \frac{25}{50} ?

Answer- Checking the value of the denominators is the first step in identifying the rational numbers between two rational numbers.

Here, both rational numbers have the same denominator.

Because of this, the 3 rational numbers between them are \frac{22}{50} , \frac{23}{50} , and \frac{24}{50} .

2. Find one rational number between \frac{9}{12} and \frac{11}{15} ?

Answer-

Let's determine the LCM of the denominators of the corresponding 2 rational numbers since their denominators are different.

LCM(12,15)= 60

We divide and multiply \frac{9}{12} by 5, we get \frac{45}{60} .

We divide and multiply \frac{11}{15} by 4, we get \frac{44}{60} .

Multiply and divide both rational numbers by 10, we get \frac{450}{600} and \frac{440}{600}.

One rational number between two rational numbers is \frac{441}{600} .