70000 In Words
Introduction

To say or write "70000" in words, you have to understand the meaning of "70000" first. At first glance, “70000” appears to be a number. Isn’t it right?
What will happen in case you put some “unit of measurement” (like a g, an ml, etc.) along with "70000"? It will, then, indicate some physical quantity (like "70000 g" of chocolate cake, or "70000 ml” of oil).
As such, "70000" as a number is made up of the digits 7, 0, 0, 0, and 0; and every digit changes its meaning with the change of its place value in the number. Let us dive into it to explore further.
How Do You Define Numbers In A Decimal Number System?
You can translate any number into words in the decimal numbering system, only when you spot the position of each digit in the number. This position of every digit indicates its unique place value and thus defines the number.
The place value of each digit in a number in the decimal number system is ascertained based on the universal reference from the rightmost digit. You will get the place value gradually increasing by “a power of 10” as you move to the left direction from the “rightmost digit of the number”.
Ten crore’s place value | crore place value | Ten lakh’s place value | lakh place value | Ten thousandth place value | Thousandth place value | Hundredth place value | Ten’s place value | Unit or One’s place value |
\[{{10}^{8}}\]
| \[{{10}^{7}}\]
| \[{{10}^{6}}\]
| \[{{10}^{5}}\]
| \[{{10}^{4}}\]
| \[{{10}^{3}}\]
| \[{{10}^{2}}\]
| \[{{10}^{1}}\]
| \[{{10}^{1}}\]
|
How Do You Say "70000" In Words?
At first glance, it is evident that "70000" has no unit of measurement accompanying it. So, clearly "70000" is a unitless number only.
There are “5” digits in the number "70000".
In line with the decimal number system, you have the following findings for the place values of these 5 digits of "70000".
The unit’s place in the number "70000" is "0".
The ten’s place in the number "70000" is "0".
The hundredth place in the number "70000" is "0"
The thousandth place in the number "70000" is "0".
The ten thousandth place in the number "70000" is “7”.
Place value for Ten thousand | Place value for Thousands | Place value for hundreds | Ten’s place value | Unit or One’s place value |
7\times {{10}^{4}}
| 0\times {{10}^{3}}
| 0\times {{10}^{2}}
| 0\times {{10}^{1}}
| 0\times {{10}^{0}}
|
Mathematically you can deduce the following
\[\begin{align}
7\times {{10}^{4}}+0\times {{10}^{3}}+0\times {{10}^{2}}+0\times {{10}^{1}}+0\times {{10}^{0}} \\
=7\times {{10}^{4}} \\
=70000
\end{align}\]

Here, you can easily notice the single non-zero digit “7” in the ten thousandth place of "70000"; while all of its thousandth place, hundredth place, ten’s place, and unit’s place have the digits as zeroes only.
Therefore, to express "70000" in words, you write it in terms of ten thousand only, as per the decimal number system.
Thus, you can say that "70000" is written as “Seventy Thousand” in words.
HOW DO YOU WRITE "70,000 RUPEES” IN WORDS?
In the term "70,000 rupees” you can see that the unit "rupees" follows the number "70000".
You can, now mention the number using words and insert the unit “rupees“ following it.
So, you get that "70,000 rupees” is written as “Seventy Thousand rupees” in words.
Is "70000" An Even Number Or An Odd Number?
The fact is that any number that the number “2” completely divides, is called an “even number”, and the number that is not completely divisible by 2, but leaves a remainder, is an “odd number”.
Now, there exists no remainder in the following division of the number "70000" by “2”.
\[70000\div 2=35000\].
![]()
So, you conclude that “70000” is not at all an odd number but is, definitely, an “even number”.
Is "70000" A Perfect Square Number?
See that when you can multiply any number by itself only once, the resultant product is a “perfect square number”. In other words “a perfect square” is the product of two equal integers.
\[70000={{2}^{4}}\times {{5}^{4}}\times 7\]
![]()
Here the number "70000" cannot be expressed as the product of two equal integers. Therefore, the number "70000" is not a perfect square.
Is "70000" A Perfect Cube Number?
Whenever you multiply any number by itself twice, the product that you obtain is a “perfect cube number”. Basically, a “perfect cube number” is equal to the product of three equal integers.
\[70000={{2}^{4}}\times {{5}^{4}}\times 7\]
![]()
Here "70000" is not equal to the product of three equal integers. So, the number "70000" is not a perfect cube.
Is The Number "70000" A Prime Or A Composite?
Note that, on factorization, when any number yields two factors only (the number itself and “1”), you refer to it as a “prime number”.
When you find any number that results in more than two factors on factorization, you get a “composite number”.
\[\text{Factors of 70}000=\ 1,\ 2,\ 5,\ 7,\ 10,\ 14,\ 20,\ \ldots\ 70000\]
![]()
Here you find more than two factors of the number "70000". Hence, you get that "70000" is not a prime number, but a “composite number”.
Can You Write "70000" As An Ordinal Number?
Look to denote any place or position in a set, series, or collection, when you use any number; you add the extension “rd” or “th” or “st” (as suitable) after its numeric value. Such a number is an “ordinal number”. For example: 1st, 2nd, 3rd, 4th, and so on.
So, you can, correctly, call "70000th" as an “ordinal number”.
Is The Number "70000" Cardinal?
Any natural or counting number is, basically, a “cardinal number”.
The specific counting number "70000" is definitely, a “cardinal number”.
Frequently Asked Questions (FAQs)
You can express "70000" in the defining fractional form of “p/q” where p is any integer and, q is a non-zero integer. Thus, the number "70000" is a rational number
\[\begin{align}
70000=\frac{70000}{1} \\
=\frac{p}{q},\text{where}\ p=70000,\ q=1\left( \ne 0 \right)
\end{align}\]
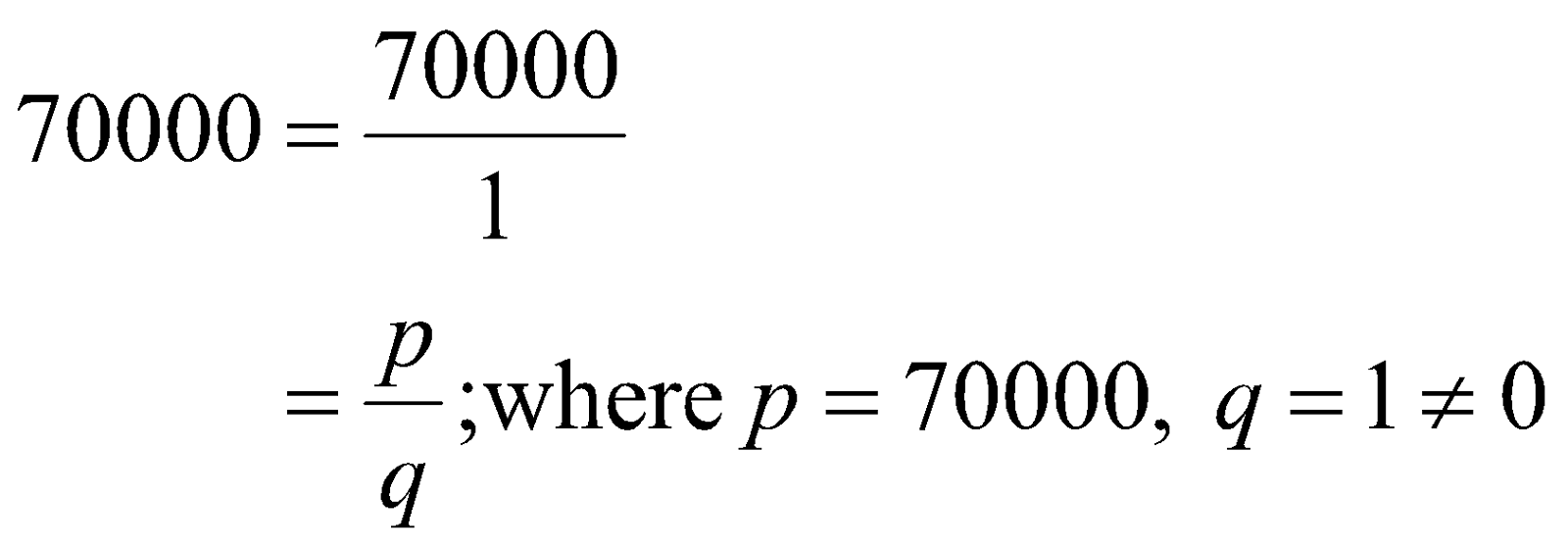
Yes, you can, definitely, show that "70000" is comprising the real part "70000" and, its imaginary part is “0”. Thus it can be expressed as a complex number.
\[70000=70000+i.0\] ![]()
Yes, the number "70000" falls in the group of the natural numbers of the number, and so, it is a natural number.
\[\begin{align}
N=\left\{ \ 1,\ 2,\ 3,\ \ldots +\infty \right\},\text{ where} \\
\infty \text{ denotes infinity and + indicates positive value or direction} \\
\end{align}\]
![]()
You may represent any number in terms of the product of its constituent digits and its corresponding place value multiplier. For ex.
7 at unit’s place gives the value 7.
But, 7 at ten’s place gives the value 70.
While 7 at hundred’s place gives the value 700.
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters