Lens Formula - Calculating Magnification Formula, FAQs

Q: What is the magnification formula of a lens?

$m=\frac{h_i}{h_o}=\frac{v}{u}$

Q: Which of the following materials cannot be used to manufacture a lens?

Water and glass are both transparent materials. A certain quantity of plastic is transparent, allowing it to be used to produce any lens; however, clay is an opaque substance that does not allow light to pass through it, so it cannot be used to make a lens.

Q: In physics, what is a lens?

A lens is a transmissive optical device that employs refraction to distribute or focus a light beam. A simple lens is made up of a single piece of transparent material, whereas a compound lens is made up of numerous simple lenses or pieces organised along a common axis.

Q: What do V and U stand for in the mirror formula?

If an object is positioned u cm in front of a spherical mirror with a focal length f and the image is produced v cm from the mirror, the equation 1/f= 1/u + 1/v is used to relate u, v, and f. The mirror formula is the name given to this equation. Both concave and convex mirrors follow the same formula.

Q: In which mirror image is the mirror image always upright?

A virtual and erect image is always formed by a convex mirror. In comparison to the object, the image is much smaller.

Q: What is the S.I. unit of magnification?

It has no unit since it is the ratio of length.

Q: What if magnification is 1?

It means the image size is the same as the size of the object.

Q: What is the magnification of a concave lens?

The magnification of the concave lens is always positive but always less than 1.

Q: How does the magnification formula relate to the lens formula?

The magnification formula m = -v/u is directly related to the lens formula. It uses the image distance (v) and object distance (u) to determine how much larger or smaller the image is compared to the object. The negative sign indicates image inversion.

Lens Formula - Calculating Magnification Formula, FAQs

Edited By Vishal kumar | Updated on Jul 02, 2025 04:31 PM IST

The lens magnification formula is a fundamental concept in optics, playing a crucial role in understanding how lenses affect the appearance of objects. Magnification, defined as the ratio of the image size to the object size, helps us determine how much larger or smaller an object appears when viewed through a lens. This article will explore what is lens formula, magnification, derivation of lens magnification formula, its application in real-world scenarios, and its significance in both scientific and daily contexts.

This Story also Contains

What is Lens Formula?
Define Magnification And Magnification Formula
Magnification
Magnification Of Convex Lens
Magnification of Concave Lens
Practical Applications Of Magnification Of Lens
Power Of Lens Formula

Lens Formula - Calculating Magnification Formula, FAQs

What is Lens Formula?

In optical physics, spherical lenses are lenses made by combining two spherical surfaces. These lenses are divided into two categories based on the notion of formation by binding two surfaces: convex lenses, which are created by binding two spherical surfaces curved outward, and concave lenses, which are formed by binding two spherical surfaces curved inward.

Lens formula

Depending on the distance between the lens and the objects, the images created by these lenses can be actual, virtual, or of varied sizes. The formula of the lens now assists us in determining the picture distance. It is the formula, or the equation, that links the focal length formula, object distance, and image distance for a lens.

The Lens formula describes the relationship between the distance of an image (v), the distance of an object (u), and the focal length of the lens formula (f) of the lens in optics. The lens formula works for both convex and concave lenses. The thickness of these lenses is minimal. The following is the formula of the lens:

$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$

Where,

$v$ is the Image formation distance from the lens's optical center.
$u$ is the object's distance from the lens's optical center.
$f$ is the focal length formula of the lens.

The lens formula applies to both convex and concave lenses. It can also be used to figure out how far real and virtual images are apart. If the equation yields a negative image distance, the resulting picture is virtual and on the same side as the item. The lens is diverging rather than converging if the equation returns a negative focal length formula.

Also read -

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Define Magnification And Magnification Formula

Converging and diverging lenses are optical physics miracles that employ these media's ability to refract, reflect, or bend light beams. In general, there are two types of lenses: convex (curved outward) and concave (curved inward) (curved inward). One of its primary functions is to magnify images, making them look larger than they are. These lenses can now be found in microscopes, telescopes, binoculars, and other optical devices, as well as our own eyes. Scientists and students can use a variety of simple to complicated algebraic equations to link a lens' shape and physical characteristics to the impact it has on light rays passing through it.

Related Topics,

Magnification

Magnification is a measure of how much larger or smaller an image appears compared to the actual object.

Magnification Formula For Lens

The magnification of a lens is the ratio of the height of the image to the height of the object.

It is the ratio of image distance to that of object distance.

$\begin{aligned} m = \frac{Height of the image}{Height of the object} \\ m = \frac{h_{i}}{h_{o}} \end{aligned}$

where,

$m$ is the magnification
$h_{i}$ is the height of the image
$h_{o}$ is the height of the object

$\begin{aligned} m & = \frac{Image Distance}{Object Distance} \\ m & = \frac{v}{u} \end{aligned}$

where,

$m$ stands for magnification.
$v$ is image distance.
$u$ is the object distance

Magnification Of Convex Lens

Magnification produced by the convex lens be either positive or negative depending on the image characteristics.

convex lens

(i) Object beyond 2F

Image is real, inverted, and smaller than the object
Magnification: $| m | < 1$

(ii) Object at 2F

Image is real, inverted, same size as the object
Magnification: $| m | = 1$

(iii) Object between F and 2F

Image is real, inverted, larger than the object.
Magnification : $| m | > 1$

(iv) Object within F

Image is virtual, upright, larger than the object.
Magnification: $| m | > 1$

Magnification of Concave Lens

Magnification of a concave lens is always positive as the image formed is virtual.
The image distance is negative for virtual images
The object distance is negative according to sign convention.
The magnification is always positive: $| m | > 0$
The value of the magnification is less than one: $| m | < 1$

Practical Applications Of Magnification Of Lens

Microscopes: Use high magnification to observe small specimens
Telescopes: Magnify distant celestial objects in the sky.
Cameras: Adjust lens settings to get the desired image

Power Of Lens Formula

The ability of a lens to focus light rays falling on it is its power. In other words, it's a measurement of how close the rays of light falling on the lens are converged or diverged.
The power of a lens can be described as the reciprocal of the focal length of the lens because the degree of convergence or divergence of the rays is determined by the focal length of the lens.

$P = \frac{1}{Focal Length}$

$P = \frac{1}{f}$

The dioptre is the SI unit of lens power and is sometimes abbreviated as D. 1 dioptre is the power of a lens with a focal length of 1 meter.
For a concave lens' focal length is negative, its power is negative (-), whereas the power of a convex lens is positive (+) because its focal length is positive.

Also check-

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. What is the magnification formula of a lens?

$m = \frac{h_{i}}{h_{o}} = \frac{v}{u}$

2. Which of the following materials cannot be used to manufacture a lens?

Water and glass are both transparent materials. A certain quantity of plastic is transparent, allowing it to be used to produce any lens; however, clay is an opaque substance that does not allow light to pass through it, so it cannot be used to make a lens.

3. In physics, what is a lens?

A lens is a transmissive optical device that employs refraction to distribute or focus a light beam. A simple lens is made up of a single piece of transparent material, whereas a compound lens is made up of numerous simple lenses or pieces organised along a common axis.

4. What do V and U stand for in the mirror formula?

If an object is positioned u cm in front of a spherical mirror with a focal length f and the image is produced v cm from the mirror, the equation 1/f= 1/u + 1/v is used to relate u, v, and f. The mirror formula is the name given to this equation. Both concave and convex mirrors follow the same formula.

5. In which mirror image is the mirror image always upright?

A virtual and erect image is always formed by a convex mirror. In comparison to the object, the image is much smaller.

6. What is called magnification of the lens?

The magnification of a lens is the ratio of the height of the image to the height of the object. Also, it is the ratio of image distance to that of object distance.

7. What is the S.I. unit of magnification?

It has no unit since it is the ratio of length.

8. What if magnification is 1?

It means the image size is the same as the size of the object.

9. What is the magnification of a concave lens?

The magnification of the concave lens is always positive but always less than 1.

10. How does the magnification formula relate to the lens formula?

The magnification formula m = -v/u is directly related to the lens formula. It uses the image distance (v) and object distance (u) to determine how much larger or smaller the image is compared to the object. The negative sign indicates image inversion.

11. How does the lens formula relate to the concept of teleconverters in photography?

Teleconverters increase the effective focal length of a lens, which changes the values used in the lens formula. If a 2x teleconverter is used, the effective focal length doubles, changing how u, v, and f interact in the formula and typically increasing magnification.

12. What's the significance of the 2f point in relation to the lens formula and magnification?

The 2f point (twice the focal length) is significant because when an object is placed here, its image also forms at 2f on the opposite side of the lens. At this point, the image is real, inverted, and the same size as the object (magnification = -1).

13. What happens to magnification in a telecentric lens system?

In a telecentric lens system, magnification remains constant regardless of object distance. This is achieved by placing the aperture stop at the focal point of the lens. The standard magnification formula still applies, but the ratio v/u remains constant as the object moves.

14. How does the lens formula change for gradient-index (GRIN) lenses?

GRIN lenses have a varying refractive index throughout the material, causing light to bend continuously rather than at discrete surfaces. The simple lens formula doesn't apply; instead, ray tracing or wave optics approaches are needed to determine image formation and magnification.

15. What does a magnification of 1 mean?

A magnification of 1 means the image is the same size as the object. This occurs when the object distance equals the image distance (u = v) in the magnification formula m = -v/u.

16. What happens to magnification in a zoom lens system?

In a zoom lens system, the focal length can be varied, changing the magnification. As the focal length increases, so does the magnification for a given object distance. The lens formula and magnification formula still apply, but with a variable f value.

17. How does the lens formula change for anamorphic lenses?

Anamorphic lenses have different focal lengths in horizontal and vertical directions, used to create widescreen images. The lens formula must be applied separately for each direction, resulting in different magnifications horizontally and vertically.

18. What happens to the image when the object is placed exactly at the focal point of a converging lens?

When the object is placed exactly at the focal point of a converging lens, the image theoretically forms at infinity. The rays emerge parallel from the lens, resulting in no real image formation. This scenario represents the transition between real and virtual image formation.

19. How does the magnification formula change for compound microscopes?

For a compound microscope, the total magnification is the product of the objective lens magnification and the eyepiece magnification. Each lens's magnification is calculated using the standard formula m = -v/u, but the overall system magnification is their product.

20. Can magnification ever be positive?

Yes, magnification can be positive for virtual images. This occurs when the image is on the same side of the lens as the object and is not inverted. Common examples include images formed by convex lenses when the object is within the focal length.

21. What happens to magnification as an object approaches a converging lens?

As an object approaches a converging lens, the magnification increases. When the object is beyond 2f, the image is smaller than the object. At 2f, the image is the same size. Between f and 2f, the image is larger but inverted. Within f, a larger virtual image forms.

22. What happens to the image when the object is placed at twice the focal length of a converging lens?

When the object is placed at twice the focal length (2f) of a converging lens, the image forms at 2f on the opposite side of the lens. The image is real, inverted, and the same size as the object (magnification = -1).

23. How does astigmatism affect the lens formula and magnification?

Astigmatism occurs when a lens has different focal lengths in different planes. This means the simple lens formula doesn't apply uniformly across the lens surface. Magnification can vary across the image, leading to distortion, particularly noticeable in the periphery of the image.

24. What's the relationship between magnification and field of view?

As magnification increases, the field of view generally decreases. This is because higher magnification means focusing on a smaller area of the object, resulting in less of the surrounding area being visible in the image.

25. What's the relationship between magnification and image type (real vs. virtual)?

For real images formed by converging lenses, magnification is negative and the image is inverted. For virtual images (formed by diverging lenses or by converging lenses when the object is within the focal length), magnification is positive and the image is upright.

26. Can you have a magnification between 0 and 1?

Yes, a magnification between 0 and 1 (exclusive) indicates that the image is smaller than the object but not inverted. This occurs with real images formed by converging lenses when the object is beyond 2f, or with virtual images formed by diverging lenses.

27. Why is the magnification negative for real images?

The magnification is negative for real images because they are inverted compared to the object. This inversion is represented mathematically by the negative sign in the magnification formula m = -v/u.

28. What happens to magnification as the object distance approaches infinity?

As the object distance (u) approaches infinity, the magnification (m = -v/u) approaches zero. This means very distant objects produce very small images, which is why distant objects appear small to our eyes and in photographs.

29. How does spherical aberration affect the lens formula and magnification?

Spherical aberration causes light rays passing through different parts of the lens to focus at slightly different points. This means the simple lens formula is not equally accurate for all parts of the lens, potentially leading to variations in magnification and image quality across the image.

30. How does the index of refraction of the lens material affect the focal length?

A higher index of refraction increases the lens's ability to bend light, resulting in a shorter focal length for a given lens shape. This relationship is described by the lensmaker's equation, which relates the focal length to the lens's curvature and refractive index.

31. How does the lens formula change for a system of two thin lenses?

For a system of two thin lenses in contact, the effective focal length (f) is given by 1/f = 1/f₁ + 1/f₂, where f₁ and f₂ are the focal lengths of the individual lenses. This combined focal length can then be used in the standard lens formula.

32. How does the lens formula relate to the concept of optical power?

Optical power (P) is the reciprocal of focal length (f) in meters: P = 1/f. The lens formula can be rewritten in terms of power as P = 1/u + 1/v. This form is particularly useful when dealing with multiple lenses, as powers can be added directly.

33. How does changing the focal length affect magnification?

Changing the focal length while keeping the object distance constant will change the image distance and thus the magnification. A shorter focal length (stronger lens) will generally produce a larger magnification for a given object distance.

34. How does chromatic aberration affect the lens formula and magnification?

Chromatic aberration occurs because different wavelengths of light have slightly different focal lengths in a lens. This means the lens formula and magnification will vary slightly for different colors, leading to color fringes in images, especially at high magnifications.

35. How can you use the lens and magnification formulas to find an unknown focal length?

If you know the object distance (u), image distance (v), and magnification (m), you can use the magnification formula to verify v/u, then plug u and v into the lens formula 1/f = 1/u + 1/v to solve for the unknown focal length f.

36. What's the difference between linear and angular magnification?

Linear magnification (m = -v/u) refers to the ratio of image size to object size. Angular magnification, used for optical instruments like telescopes, refers to the ratio of the angle subtended by the image to the angle subtended by the object at the unaided eye.

37. Can you have infinite magnification?

Theoretically, infinite magnification occurs when an object is placed exactly at the focal point of a converging lens. In this case, the image forms at infinity. However, in practice, limitations like lens imperfections and diffraction prevent truly infinite magnification.

38. Can the magnification formula be used for mirrors?

Yes, the magnification formula m = -v/u applies to both lenses and mirrors. For mirrors, a negative magnification indicates an inverted image, while a positive magnification indicates an upright image, just as with lenses.

39. What's the difference between lateral and longitudinal magnification?

Lateral magnification (m = -v/u) refers to the ratio of image height to object height perpendicular to the optical axis. Longitudinal magnification refers to the ratio of the image's depth to the object's depth along the optical axis. They're not always equal, leading to distortion in some optical systems.

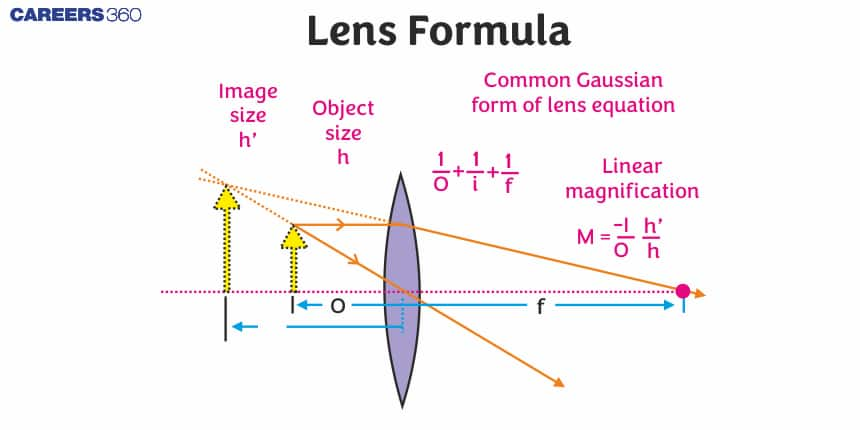
40. What is the lens formula and how is it used?

The lens formula is 1/f = 1/u + 1/v, where f is the focal length of the lens, u is the object distance, and v is the image distance. It's used to relate these three quantities for any thin lens, allowing you to calculate one value if you know the other two.

41. How does the sign convention work in the lens formula?

In the lens formula, distances are positive if they're on the side of the lens where light enters (the "real" side) and negative on the other side. For a real image, v is positive. For a virtual image, v is negative. The focal length f is positive for converging lenses and negative for diverging lenses.

42. How does the lens formula relate to the mirror formula?

The lens formula (1/f = 1/u + 1/v) and the mirror formula (1/f = 1/u + 1/v) are identical in form. However, the sign conventions differ. For mirrors, distances are positive in front of the mirror and negative behind it, while for lenses, distances are positive on the side where light enters.

43. Why doesn't the lens formula work for thick lenses?

The lens formula assumes thin lenses where light rays effectively bend at a single plane. Thick lenses have two refracting surfaces separated by a significant distance, causing additional refraction and changing the effective focal length, making the simple thin lens formula inaccurate.

44. How does the lens equation change for a diverging lens?

The lens equation remains the same (1/f = 1/u + 1/v), but for a diverging lens, the focal length f is negative. This means that for real objects, the image will always be virtual, upright, and smaller than the object.

45. Why do we use the thin lens approximation?

The thin lens approximation simplifies calculations by assuming all refraction occurs at a single plane. This is valid when the lens thickness is much smaller than the object and image distances, allowing us to use the simple lens formula without considering the lens's internal structure.

46. How does the lens formula change for non-air mediums?

When the lens is surrounded by a medium other than air, the lens formula becomes (n₂ - n₁)/f = n₂/u + n₂/v, where n₁ is the refractive index of the lens material and n₂ is the refractive index of the surrounding medium.

47. What's the significance of the 1/f term in the lens formula?

The 1/f term in the lens formula represents the optical power of the lens. It determines how strongly the lens converges or diverges light. A larger 1/f value (smaller f) indicates a stronger lens that bends light more sharply.

48. How does the lens formula relate to the concept of conjugate points?

Conjugate points are pairs of points where an object at one point produces an image at the other. The lens formula relates these points: for any pair of conjugate points (u and v), the formula 1/f = 1/u + 1/v holds true.

49. What's the relationship between f-number and the lens formula?

The f-number (N) is defined as the ratio of focal length to lens diameter: N = f/D. While not directly part of the lens formula, it affects the amount of light gathered and the depth of field, which can impact image quality and effective magnification in practical applications.

50. How does the lens formula change for a thick lens?

For a thick lens, the simple thin lens formula is replaced by a more complex equation that takes into account the lens thickness and the refractive indices of the lens material and surrounding medium. The concept of principal planes is introduced to simplify calculations.

51. What's the relationship between the lens formula and the concept of vergence?

Vergence is the reciprocal of distance and is measured in diopters (1/m). The lens formula can be expressed in terms of vergence: V_f = V_o + V_i, where V_f is the lens vergence (1/f), V_o is the object vergence (1/u), and V_i is the image vergence (1/v).

52. What's the significance of the sign of the image distance (v) in the lens formula?

The sign of the image distance (v) indicates whether the image is real or virtual. A positive v means the image is on the opposite side of the lens from the object (real image), while a negative v means the image is on the same side as the object (virtual image).

53. How does the lens formula relate to the concept of depth of field?

While the lens formula doesn't directly calculate depth of field, it's related. The formula helps determine the image distance for a given object distance. The depth of field is the range of object distances that produce acceptably sharp images at this image distance, affected by factors like aperture and focal length.

54. How does the lens formula change for non-spherical lenses?

For non-spherical lenses (like parabolic or aspherical lenses), the simple lens formula doesn't apply accurately. These lenses are designed to reduce aberrations, but their behavior is more complex and often requires ray tracing or advanced optical modeling to predict image formation and magnification.

55. What's the relationship between the lens formula and the concept of working distance in microscopy?

The working distance is the space between the front of the objective lens and the focal plane of the specimen. It's related to the object distance (u) in the lens formula. Shorter focal length objectives generally have smaller working distances, affecting how the lens formula is applied in practical microscopy.

56. How does the lens formula relate to the concept of numerical aperture?

While not directly part of the lens formula, numerical aperture (NA) affects the resolving power and light-gathering ability of a lens. Higher NA lenses can resolve finer details, which can impact the effective magnification and image quality in practical applications.

57. What's the relationship between the lens formula and the concept of hyperfocal distance?

The hyperfocal distance is the nearest distance at which a lens can be focused while keeping objects at infinity acceptably sharp. It's related to the lens formula as it depends on focal length, but also involves factors like aperture and acceptable circle of confusion, which aren't part of the basic formula.

58. How does the lens formula change for Fresnel lenses?

Fresnel lenses use a series of concentric grooves to achieve the optical properties of a much thicker lens. While the basic lens formula still applies for the overall behavior, the detailed image formation is more complex due to the discontinuous surface.

59. What's the significance of the sign of focal length (f) in the lens formula?

The sign of the focal length indicates whether the lens is converging (positive f) or diverging (negative f). This affects how the lens formula is interpreted: converging lenses can form both real and virtual images, while diverging lenses only form virtual images for real objects.