Derivation of Mirror Formula

Edited By Team Careers360 | Updated on May 27, 2022 01:48 PM IST

Define Mirror Formula.

A mirror equation relates object distance and image distance to focal length. It's sometimes referred to as mirror formula. The object distance, image distance, as well as focal length is connected in ray optic and the proof of mirror formula is given as follows:
$\frac{1}{f}=\frac{1}{u}+\frac{1}{v}$

Assumptions in deriving the mirror equation derivation:

To derive the mirror formula derivation, the following assumptions are made.

The distances are calculated from the mirror's pole.
The negative sign represents the distance measured in the direction opposing the incident ray, whereas the positive sign indicates the distance measured in the direction of the incident ray, according to convention.
Negative distances are below the axis, whereas positive distances are above it.

Latest: JEE Main: high scoring chapters | Past 10 year's papers

Don't Miss: Most scoring concepts for NEET | NEET papers with solutions

New: Aakash iACST Scholarship Test. Up to 90% Scholarship. Register Now

Also read -

Sign convention for spherical mirrors:

Cartesian Sign Convention:

In the case of a spherical mirror, all signs are taken from the pole, which is often referred to as the origin or origin point. The New Cartesian Sign Convention is the name given to this sign convention.

From the pole of a spherical mirror towards the object along the primary axis, the sign is ⁻ (negative). In front of a spherical mirror, this means that the sign is always taken as ⁻ (negative). For example, in both types of spherical mirrors, i.e. concave and convex mirrors, the object distance is always taken as ⁻ (negative).

Behind the spherical mirror, the sign is read as ⁺ (positive). For example, if an image is generated behind the mirror, the image's distance from the pole along the principal axis is considered as ⁺ (positive).

The height of is measured above the principal axis as ⁺(positive) and below the principal axis as ⁻ (negative).

In the case of a mirror formula for concave mirror,

The object distance is always negative because the object is always situated in front of the mirror.

Because the mirror formula for concave mirror's centre of curvature and focus are in front of it, the radius of curvature and focal length are negative in this situation.

When an image is formed in front of a mirror, the distance between the image and the mirror is ^– (negative), and when an image is formed behind a mirror, the distance between the image and the mirror is ⁺ (positive) (positive).

In the case of an erect image, the height is positive; in the event of an inverted image, it is negative.

In the case of a convex mirror, the sign is:

Because the item is always in front of the mirror, the object distance is negative.

Because the convex mirror's centre of curvature and focus are behind it, the radius of curvature and focal length are considered as ⁺ (positive) in this situation.

Related Topics Link,

Derivation of formula for curved mirrors and derivation of mirror equation:

Derive mirror formula for concave mirror or give derivation of mirror formula for concave mirror.

Derive mirror formula for concave mirror

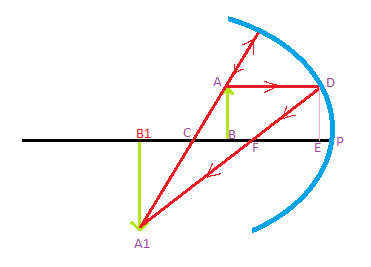
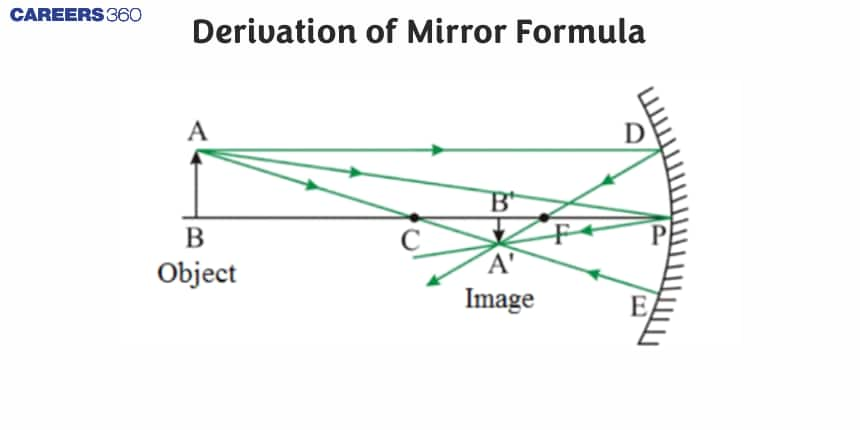
The object AB is placed at a distance of ‘u’ from P, which is the pole of the mirror, as shown in the diagram above. The image A1B1 is created at ‘v’ from the mirror, according to the diagram.

The opposite angles are equal according to the law of vertically opposite angles, as seen in the diagram above. As a result, we can write::

∠ACB=∠A₁CB₁

Similarly, ∠ABC=∠A₁B₁C ( since they are right angles).

Since the 2 angles of ∆ACB=∆A1CB1 are equal their 3^rd angle is also equal.

BAC=∠B₁A₁C

Also AB/A₁B₁=BC/B₁C ---------------(1)

Similarly ∆FED=∆FA₁B₁

So, ED/A₁B₁=EF/FB₁

Also, ED=AB

Also read :

Therefore,

AB/A₁B₁=EF/FB₁ -------------(2)

Combining equation 1 and 2

BC/B₁C=EF/FB₁

Consider that point D lies very near to point P

Therefore EF = PF

So, BC/B₁C=PF/FB₁

From the above diagram,

BC = PC-PB

B₁C = PB₁-PC

FB₁ = PB₁-PF

(PC-PB)/(PB₁-PC)=EF/(PB₁-PF) ------------------------(3)

Substituting the values and providing the signs,

PC = -R

PB =- u

PB1 = -v

PF = -f

NCERT Physics Notes :

Therefore, equation (3) becomes,

[-R-(-u)/[-v-(-R)]=-f/[-v-(-f)]

(u-R)/(R-v)=-f/(f-v)

(u-R)/R-v=f/(v-f)

On solving the equation

uv – uf – Rv + Rf = Rf – vf

uv – uF – Rv + vf = 0

But R = 2f

uv – uf – 2fv + vf = 0

Dividing throughout by uv,

$\frac{1}{f}=\frac{1}{u}+\frac{1}{v}$

This equation is called the mirror formula derivation.

Also, check-

Frequently Asked Question (FAQs)

1. Defferentiate between a concave and convex mirror.

Mirror formula for concave mirrors are spherical mirrors with a reflecting inner surface. Convex mirrors are spherical mirrors with a reflecting outer surface.

2. What are the assumptions on deriving the mirror equation derivation?

The distances are calculated from the mirror's pole.
The negative sign represents the distance measured in the direction opposing the incident ray, whereas the positive sign indicates the distance measured in the direction of the incident ray, according to convention.
Negative distances are below the axis, whereas positive distances are above it.

3. Explain the Cartesian sign convention for spherical mirrors.

From the pole of a spherical mirror towards the object along the primary axis, the sign is − (negative). In front of a spherical mirror, this means that the sign is always taken as − (negative). For example, in both types of the spherical mirrors, i.e. concave as well as convex mirror object distance is always as negative.

Behind the spherical mirror, the sign is read as + (positive). For example, if an image is generated behind the mirror, the image's distance from the pole along the principal axis is considered as + (positive).

The height of is measured above the principal axis as + (positive) and below the principal axis as − (negative).

4. Give the equation for mirror formula derivation.

The height of is measured above the principal axis as + (positive) and below the principal axis as − (negative).