How Many Radial Nodes are Present in The 5f Orbital

Introduction

By utilizing a specific formula, one can easily determine the number of nodes present in an atom. The formula is based on the principal quantum number and azimuthal quantum number, which together determine the number of radial nodes in a given atom. These nodes help to understand the distribution of electrons within the atom, providing insight into the atom's behaviour in chemical reactions.

What is an F Atomic Orbital?

The electrons in an atom occupy specific regions in space known as atomic orbitals. These orbitals are categorized into four types: s, p, d, and f, each with distinct shapes and properties. The principal quantum number, represented by n, determines the main shell in which an electron resides. For instance, a 4s orbital denotes the fourth main shell. The f orbitals are complex in shape and can hold up to 14 electrons. They are similar in appearance to d orbitals when filled and can be further divided into three subcategories based on their alignment: two lobes for sigma bonding, six lobes for sigma and pi bonding, and eight lobes for pi or delta bonding.

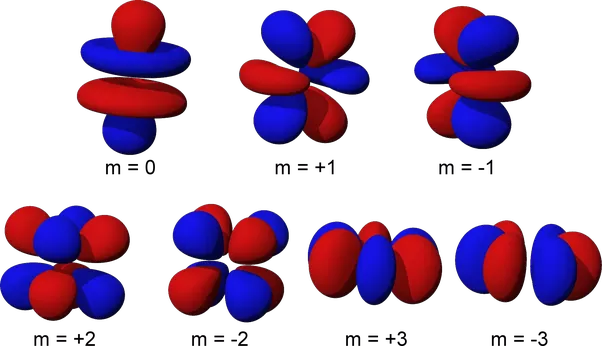
Shapes of F orbital

The f orbitals are known for their complex and unique properties, making them a vital component in understanding various chemical and physical phenomena. Additionally, the f orbitals play a significant role in the field of materials science, particularly in the development of advanced materials with unique properties such as superconductivity and magnetism. The use of f orbitals is also crucial in the field of quantum mechanics, providing a deeper understanding of the behavior of electrons and the nature of matter at the atomic level.

What are Radial Nodes?

The position of electrons in an atom is determined by the number of radial nodes present. These nodes, represented by spherical surfaces, indicate areas where the probability of finding an electron is zero. They can be calculated using the formula n-I-1, where n represents the principal quantum number and i represents the azimuthal quantum number. As the principal quantum number increases, the number of radial nodes also increases. The azimuthal quantum number is used to determine the shape of the orbital, and the number of radial nodes ultimately affects the overall distribution of electrons in the atom.

How Many Radial Nodes are Present in The 5f Orbital?

To determine the distribution of electrons in an atom, scientists use the concept of radial nodes. These nodes, also known as spherical surfaces, are points where the probability of finding an electron is zero. Radial nodes are calculated using the formula n-I-1, where n is the principal quantum number and i is the azimuthal quantum number. As the value of n increases, the number of radial nodes also increases. The azimuthal quantum number is used to determine the shape of the orbital and is written as a whole integer (s = 0, p = 1, d = 2, f = 3). Using this formula, we can determine that a 5f orbital has 1 radial node.

Conclusion

Thus, by utilizing the formula n-I-1 and inputting the values of the principal quantum number and azimuthal quantum number, it can be determined that a 5f orbital of an atom contains a single radial node. This information can be used to understand the distribution of electrons in an isolated atom and its impact on chemical phenomena.