Einstein's Explanation Of Photoelectric Effect - A Complete Guide
Albert Einstein, one of the greatest physicists, contributed his inevitable works and proposed many theories in different fields of physics like the special theory of relativity, concepts of the black hole, photoelectric effect, Einstein quantum theory, Einstein-Maxwell equation, many more topics and some other assumptions. His instinct on the theories never fails. In any field, the Albert Einstein equation plays a prominent role and the Einstein photoelectric equation can be considered as the best achievement of his work. In 1921, he received the Nobel Prize in Physics for his work Einstein theory of photoelectric effect.
JEE Main/NEET 2027: Physics Important Formulas for Class 10
NEET 2025: Mock Test Series | Syllabus | High Scoring Topics | PYQs
JEE Main: Study Materials | High Scoring Topics | Preparation Guide
JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs
- What is Einstein Theory of Photoelectric Effect?
- Einstein Explanation of Photoelectric effect:
- Photoelectric Effect Derivation
- Numerical Problems on Photoelectric Effect
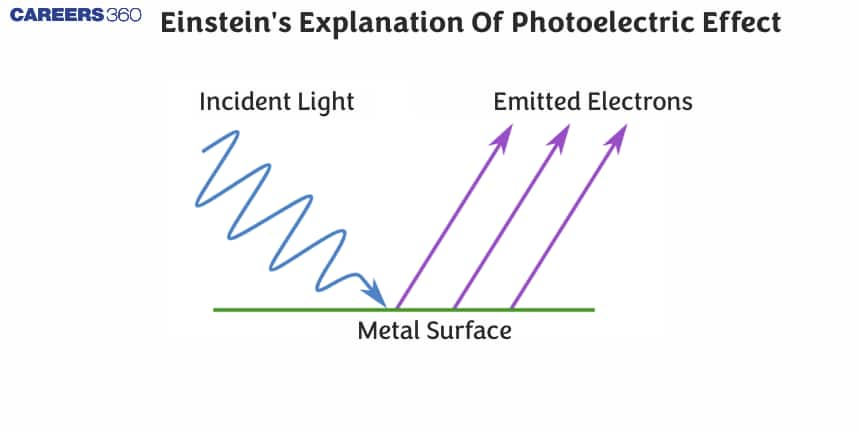
In this article, we will discuss about the Einstein photoelectric equation, derive the equation for the photoelectric effect. We'll also cover important related terms, such as threshold energy, work function, and stopping potential, with related solved numerical examples.
What is Einstein Theory of Photoelectric Effect?
The Einstein theory of photoelectric effect defines that- "Electrons are ejected from the surface of the metal when a ray of light incident on it." These ejected electrons are termed as Photoelectrons. The amount of electrons ejected from the from the surface will depends on the frequency of light incident on it. Let us discuss the explanation of Photoelectric effect.
Einstein Explanation of Photoelectric effect:
Now, let us elaborate and explain the Einstein photoelectric equation as shown in the following diagram:
- The wavy red lines represent light particles that is striking the metal surface. Energy of these photons is determined by Plank's equation:
- When the light particle (photon) hits the metal surface it transfers it energy to the electrons present on the metal surface. If this energy is greater than the work function
- The electrons will absorb the energy and leave the metal surface, as shown by the arrow directed away from the surface. These arrow represents that the electrons are leaving with Kinetic energy.
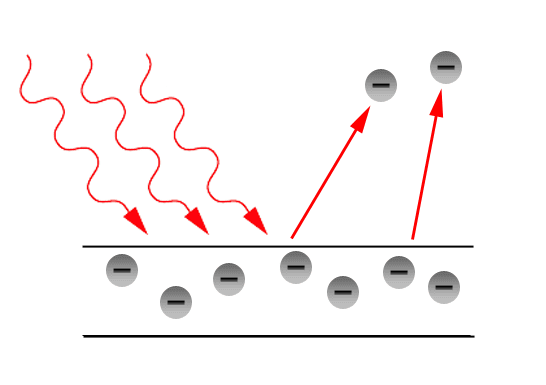
In Brief we can say that the electron will leave the metal surface if the energy provided by the photons will be greater than the work function of the metal.
If the energy provided by the photons are less than the work function, no electron is released from the metal surface.
Related Topics |
The laws of Photoelectric Emission:
- There is a minimum cutoff frequency required for emission of electrons. Below this frequency, no electron emission occurs
- The total number of emitted electrons increases with the intensity of incident light
- Kinetic energy of the electrons emitted is dependent on the frequency of light and independent of intensity of light
- There are zero time lags between the incidence of the light beam and electron emission.
Photoelectric Effect Equation
Einstein photoelectric effect equation is given by:
where:
Also read -
- NCERT Notes for all subject
- NCERT Solutions for All Subjects
- NCERT Exemplar Solutions for All Subjects
Photoelectric Effect Derivation
Let us derive Einstein’s photoelectric equation mathematically and this can be written as
Energy of photon = Energy required to remove the electron from the surface of the metal (W) + Maximum Kinetic energy of the electron which is ejected from the surface of the metal.
The energy of the incident photon (
- To remove the electron from the metal surface, which requires the work function
- To provide kinetic energy K. E. to the ejected electron.
Therefore, we can write:
Rearranging, we get:
At the threshold frequency
3. Maximum Kinetic Energy:
Substituting
or
For an electron with mass
The stopping potential
Thus:
Substituting from equation (1), we get:
This equation represents the relationship between the stopping potential
This final expression shows the Einstein photoelectric effect equation, showing how the maximum kinetic energy (or the stopping potential) depends on the frequency of the incident light and the material’s threshold frequency.
Scientific Terms in Photoelectric Effect
Threshold Frequency:
The minimum frequency of the given incident light beam which is required for the emission of electrons from the surface of the metal is known as Threshold frequency.
Work Function:
The minimum energy required in the removal of the electron from the surface of the metal is known as Work Function. It is represented by
Stopping potential:
The required potential to stop the emission of the electron from the surface of the metal is known as stopping potential. It is represented by
Numerical Problems on Photoelectric Effect
1. The threshold frequency for a certain metal is
Solution:
1. Use the formula for the work function
where
2. Substitute the values:
3. Convert this to electron volts ( eV ) by dividing by the charge of an electron,
Answer: The work function of the metal is 2.07 eV .
2- Light of wavelength 400 nm is incident on a metal surface with a work function of 2.2 eV . Will electrons be ejected from the metal surface? If yes, calculate the maximum kinetic energy of the emitted electrons. (Use
Solution:
1. First, calculate the energy of the incident photon using
2. Convert
3. Since the photon's energy ( 3.1 eV ) is greater than the work function ( 2.2 eV ), electrons will be ejected from the metal surface.
4. Calculate the maximum kinetic energy of the ejected electrons using the photoelectric equation:
Answer: Yes, electrons will be ejected, and the maximum kinetic energy of the emitted electrons is 0.9 eV .
Frequently Asked Questions (FAQs)
There is a minimum cutoff frequency required for emission of electrons. Below this frequency, no electron emission occurs
The total number of emitted electrons increases with the intensity of incident light
Kinetic energy of the electrons emitted is dependent on the frequency of light and independent of intensity of light
There are zero time lags between the incidence of the light beam and electron emission.
The Photoelectric effect can be explained by assuming that light is incident on the surface of the metal, and then the electron in the surface of the metal gets ejected. This phenomenon of photoelectric effect was explained by the Albert Einstein Photoelectric equation.
The photoelectric effect was initially explained by Heinrich Hertz in the year of 1887 and later it was preceded by Lenard in the year of 1902.
The Einstein photoelectric equation can be written as follows
Eνo= ½ (mvmax2) = h (ν - νo)
The threshold frequency formula can be written as W= hνo, where h is Planck’s constant and h = 6.626 x 10-34 J Hz-1
Also Read
02 Jul'25 06:05 PM
02 Jul'25 05:50 PM
02 Jul'25 05:31 PM
02 Jul'25 05:08 PM
02 Jul'25 05:02 PM
02 Jul'25 04:44 PM

