Biot-savart Law

The Biot-Savart Law is one of the fundamental concepts in electromagnetism which describes how magnetic fields are generated. According to Biot-Savart law, "The Magnetic Field at any point in space depends on three factors: density of the current, the distance from the particular current element and the angle between the chosen current element and the point at which we are going to measure the field." This law enables us to appreciate how magnetic fields are created by currents in live wire coils and various conductors.

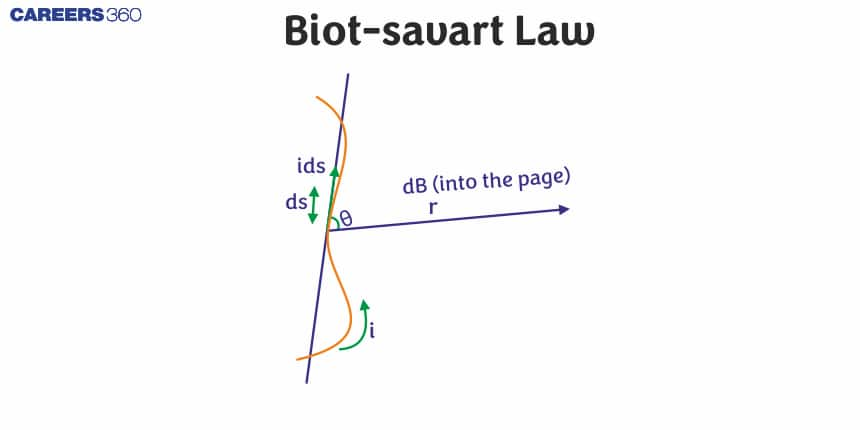
Thus, the practical significance of the Biot-Savart Law includes the use of calculation of magnetic fields of motors, generators, and inductors all of which use a controlled magnetic field to work properly. This article discusses a detail of the Biot-Savart Law, when it should be used and in detail offers several examples of its use.

Definition of Biot-Savart Law

"The Biot-Savart Law states that the magnetic field $\overrightarrow{dB}$ generated at a point in space by a small segment of current-carrying conductor $\overrightarrow{dl}$ is directly proportional to the current $I$, inversely proportional to the square of the distance $r$ between the segment and the point, and depends on the angle between $\overrightarrow{dl}$ and the line connecting the segment to the point."

The mathematical expression for the Biot-Savart Law is:

$$\overrightarrow{dB}=\frac{{\mu }_0}{4\pi }\frac{I\overrightarrow{dl}\times \overrightarrow{r}}{r^3}$$

where:
- $\overrightarrow{dB}=$ small magnetic field generated,
- ${\mu }_0=$ permeability of free space,
- $I=$ current in the conductor,
- $\overrightarrow{dl}=$ small length of the current element,
- $\overrightarrow{r}=$ vector from the current element to the point where $\overrightarrow{dB}$ is measured,
- $r=$ magnitude of $\overrightarrow{r}$.

The Biot-Savart Law helps to calculate the magnetic field produced by any shape of a current-carrying conductor.

If a point charge q is kept at rest near a current-carrying wire, It is found that no force acts on the charge. It means a current-carrying wire does not produce an electric field. However, if the charge q is projected in the direction of the current with velocity v, then it is deflected towards the wire (q is assumed positive). There must be a field at P that exerts a force on the charge when it is projected, but not when it is kept at rest. This field is different from the electric field which always exerts a force on a charged particle whether it is at rest or in motion. This new field is called the magnetic field and is denoted by the symbol B. The force exerted by a magnetic field is called magnetic force.

According to Biot Savart's Law, the magnetic induction dB at point P due to the elemental wire segment AB as shown in the figure depends upon four factors which are given as

(i) dB is directly proportional to the current in the element.

$dB\propto I$

(ii) dB is directly proportional to the length of the element

$dB\propto dl$

(iii) dB is inversely proportional to the square of the distance r of the point P from the element

$dB\propto \frac{1}{r^2}$

Combining the above factors, we have

$\begin{array}{rl}& dB\propto \frac{Idl\sin \theta }{r^2}\\ & dB=K\frac{Idl\sin \theta }{r^2}\end{array}$

Where K is a proportionality constant and its value depends upon the nature of the medium surrounding the current carrying wire. Its SI Units its value is given as

$K=\frac{{\mu }_0}{4\pi }={10}^{-7}\mathrm{T}-\mathrm{m}/\mathrm{A}$

Here, i is the current, $d\overrightarrow{l}$ is the length-vector of the current element and $\overrightarrow{r}$ is the vector joining the current element to the point P and $\theta$ is the angle between $d\overrightarrow{l}$ and $\overrightarrow{r}$.
${\mu }_0$ is called the permeability of vacuum or free space. Its value is $4\pi \times {10}^{-7}\mathrm{T}-\mathrm{m}/\mathrm{A}$.
The magnetic field at a point $P$, due to a current element in a vacuum, is given by:

Vector form:
$d\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\frac{(id\overrightarrow{l}\times \overrightarrow{r})}{r^3}$

Scalar form:
$dB=\frac{{\mu }_0}{4\pi }\frac{idl\sin \theta }{r^2}$

For medium other than vacuum, ${\mu }_0$ will be replaced by $\mu$

$\mu ={\mu }_0\times {\mu }_r$

Where: ${\mu }_r$ is the relative permeability of the medium (also known as the diamagnetic constant of the medium)

The Direction of the Magnetic Field

1. The rule of cross product

The direction of the field is perpendicular to the plane containing the current element and the point $P$ according to the rules of cross-product. If we place the stretched right-hand palm along $d\overrightarrow{l}$ in such a way that the fingers curl towards $\overrightarrow{r}$, the cross product $d\overrightarrow{l}\times \overrightarrow{r}$ is along the thumb. Usually, the plane of the diagram contains both $d\overrightarrow{l}$ and $\overrightarrow{r}$. The magnetic field $d\overrightarrow{B}$ is then perpendicular to the plane of the diagram, either going into the plane or coming out of the plane. We denote the direction going into the plane by an encircled cross and the direction coming out of the plane by an encircled dot.

2. Right-hand thumb rule

The direction of this magnetic induction is given by the right-hand thumb rule stated as "Hold the current carrying conductor in the palm of the right hand so that the thumb points in the direction of the flow of current, then the direction in which the fingers curl, gives the direction of magnetic field lines"

Cases:

Case 1. If the current is in a clockwise direction then the direction of the magnetic field is away from the observer or perpendicular inwards.

Case 2. If the current is in an anti-clockwise direction then the direction of the magnetic field is towards the observer or perpendicular outwards

Magnetic Field Due to Current in a Straight Wire

Magnetic field lines around a current-carrying straight wire are concentric circles whose centre lies on the wire.

The magnitude of magnetic field B, produced by a straight current-carrying wire at a given point is directly proportional to the current I pairing through the wire i.e. B is inversely proportional to the distance 'r' from the wire \left(B \propto \frac{1}{r}\right) as shown in the figure given below.

Derivation

The directions of magnetic fields due to all current elements are the same in the figure shown, we can integrate the expression of magnitude as given by Biot-Savart law for the small current element dy as shown in the figure

$B=\int \mathrm{dB}=\frac{{\mu }_0}{4\pi }\int \frac{Idy\sin \theta }{x^2}$

In order to evaluate this integral in terms of angle $\phi$, we determine đy, x and \theta in terms of perpendicular distance "r" (which is a constant for a given point) and angle " $\varphi$". Here,

$\begin{array}{rl}y& =r\tan \varphi \\ dy& =r{\sec }^2\varphi d\varphi \\ x& =r\sec \varphi \\ \theta & =\frac{\pi }{2}-\varphi \end{array}$

Substituting in the integral, we have :

$\Rightarrow B=\frac{{\mu }_0}{4\pi }\int \frac{Ir{\sec }^2\varphi d\varphi \sin (\frac{\pi }{2}-\varphi )}{r^2{\sec }^2\varphi }=\frac{{\mu }_0}{4\pi }\int \frac{I\cos \varphi d\varphi }{r}$

Taking out I and r out of the integral as they are constant:
$\Rightarrow B=\frac{{\mu }_{0}I}{4\pi r}\int \cos \varphi d\varphi$

Integrating between angle $-{\varphi }_1$ and ${\varphi }_2$, we have
$\begin{array}{c}\Rightarrow B=\frac{{\mu }_{0}I}{4\pi r}{\int }_{-{\varphi }_1}^{{\varphi }_2}I\cos \varphi d\varphi \\ \Rightarrow B=\frac{{\mu }_{0}I}{4\pi r}(\sin {\varphi }_2-\sin (-{\varphi }_1))\end{array}$

Note: $-{\varphi }_1$ is taken because it is measured in the opposite sense of ${\varphi }_2$ with respect to the reference line ( negative x-axis here)

$\Rightarrow B=\frac{{\mu }_{0}I}{4\pi r}(\sin {\varphi }_2+\sin {\varphi }_1)$

Magnetic field due to a current-carrying wire at a point P which lies at a perpendicular distance r from the wire, as shown, is given as:

$B=\frac{{\mu }_0}{4\pi }\frac{i}{r}(\sin {\varphi }_1+\sin {\varphi }_2)$

From figure, $\alpha =({90}^{\circ }-{\varphi }_1)$ and $\beta =({90}^{\circ }+{\varphi }_2)$
Hence, it can be also written as $B=\frac{{\mu }_o}{4\pi }\frac{i}{r}(\cos \alpha -\cos \beta )$

Different Cases

Case 1: When the linear conductor XY is of finite length and the point P lies on its perpendicular bisector as shown

$B=\frac{{\mu }_0}{4\pi }\cdot \frac{i}{r}(2\sin \varphi )$

Case 2: When the linear conductor XY is of infinite length and the point P lies near the centre of the conductor

$B=\frac{{\mu }_0}{4\pi }\frac{i}{r}[\sin {90}^{\circ }+\sin {90}^{\circ }]=\frac{{\mu }_0}{4\pi }\frac{2i}{r}$

Case 3: When the linear conductor is of semi-infinite length and the point P lies near the end Y or X

$B=\frac{{\mu }_0}{4\pi }\frac{i}{r}[\sin {90}^{\circ }+\sin 0^{\circ }]=\frac{{\mu }_0}{4\pi }\frac{i}{r}$

Case 4: When point P lies on the axial position of the current-carrying conductor then the magnetic field at P,

$B=\frac{{\mu }_o}{4\pi }\frac{i}{r}(\cos \alpha -\cos \beta )=\frac{{\mu }_o}{4\pi }\frac{i}{r}(\cos 0-\cos 0)=0$

Note:

• The value of magnetic field induction at a point, on the centre of separation of two linear parallel conductors carrying equal currents in the same direction, is zero.
• If the direction of the current in the straight wire the known then the direction of the magnetic field produced by a straight wire carrying current is obtained by Maxwell's right-hand thumb rule.

Magnetic Field Due to Circular Current Loop at Its Centre

Magnetic Field due to circular coil at Centre

Consider a circular coil of radius a and carrying current I in the direction shown in Figure. Suppose the loop lies in the plane of the paper. It is desired to find the magnetic field at the centre O of the coil. Suppose the entire circular coil is divided into a large number of current elements, each of length dl.

According to Biot-Savart law, the magnetic field $d\overrightarrow{B}$ at the centre O of the coil due to the current element $I\overrightarrow{dl}$ is given by,
$\overrightarrow{\mathrm{dB}}=\frac{{\mu }_0\mathrm{I}(\overrightarrow{\mathrm{di}}\times \overrightarrow{r^2})}{4\pi {\mathrm{r}}^3}$

where $\overrightarrow{r}$ is the position vector of point $O$ from the current element. The magnitude of $\overrightarrow{\mathrm{dB}}$ at the centre $O$ is
$\begin{array}{rl}& \mathrm{dB}=\frac{{\mu }_0\mathrm{Idlr}\sin \theta }{4\pi {\mathrm{r}}^3}\\ & \therefore \mathrm{dB}=\frac{{\mu }_0\mathrm{I}l\sin \theta }{4\pi {\mathrm{r}}^2}\end{array}$

The direction of $\overrightarrow{\mathrm{dB}}$ is perpendicular to the plane of the coil and is directed inwards. Since each current element contributes to the magnetic field in the same direction, the total magnetic field B at the centre O can be found by integrating the above equation around the loop i.e.

$\therefore \mathrm{B}=\int \mathrm{dB}=\int \frac{{\mu }_0\mathrm{Id}l\sin \theta }{4\pi {\mathrm{r}}^2}$

For each current element, angle between $\overrightarrow{\mathrm{dI}}$ and $\overrightarrow{r}$ is ${90}^{\circ }$. Also distance of each current element from the centre O is a.

$\begin{array}{rl}& \therefore B=\frac{{\mu }_{0}I\sin {90}^{\circ }}{4\pi {\mathrm{r}}^2}\int \mathrm{d}l\\ & \text{ But }\int \mathrm{dl}=2\pi \mathrm{r}=\text{ total length of the coil }\\ & \therefore B=\frac{{\mu }_{0}I}{4\pi {\mathrm{r}}^2}2\pi \mathrm{r}\\ & \therefore B=\frac{{\mu }_{0}I}{2\mathrm{r}}\end{array}$

For N turns,
$B_0=B_{\text{Centre }}=\frac{{\mu }_0}{4\pi }\frac{2\pi Ni}{r}=\frac{{\mu }_{0}Ni}{2r}$

where N=number of turns, i= current and r=radius of a circular coil.

Magnetic field due to a current-carrying circular arc

Case 1: Arc subtends angle theta at the centre as shown below then $B_0=\frac{{\mu }_0}{4\pi }\frac{i\theta }{r}$

Proof:

Consider length element dl lying always perpendicular to $\overrightarrow{r}$.
Using the Biot-Savart law, the magnetic field produced at $O$ is:
$$\begin{array}{rl}\overrightarrow{dB}& =\frac{{\mu }_0}{4\pi }\frac{Id\overrightarrow{l}\times \overrightarrow{r}}{r^3}\\ dB& =\frac{{\mu }_0}{4\pi }\frac{Idlr\sin {90}^{\circ }}{r^3}=\frac{{\mu }_0}{4\pi }\frac{Idl}{r^2}\dots (1)\end{array}$$

Equation (1) gives the magnitude of the field. The direction of the field is given by the right-hand rule. Thus, the direction of each of the dB is into the plane of the paper. The total field at O is

The angle subtended by element $dl$ is $d\theta$ at pt. O , therefore $dl=rd\theta$
$\begin{array}{rl}& \mathrm{B}=\int \mathrm{dB}=\frac{{\mu }_0}{4\pi }I{\int }_0^{\theta }\frac{\mathrm{d}l}{{\mathrm{r}}^2}\\ & B=\frac{{\mu }_0}{4\pi }I{\int }_0^{\theta }\frac{\mathrm{rd}\theta }{{\mathrm{r}}^2}=\frac{{\mu }_0}{4\pi }\frac{\mathrm{I}}{\mathrm{r}}\theta \dots .\end{array}$
where the angle $\theta$ is in radians.

Case 2: Arc subtends angle $(2\pi -\theta )$ at the centre then $B_0=\frac{{\mu }_0}{4\pi }\cdot \frac{(2\pi -\theta )i}{r}$

Case 3:The magnetic field of the Semicircular arc at the centre is $B_0=\frac{{\mu }_o}{4\pi }\frac{\pi i}{r}=\frac{{\mu }_{o}i}{4r}$

Case 4: Magnetic field due to three-quarter Semicircular Current-Carrying arc at the centre $B_0=\frac{{\mu }_o}{4\pi }\frac{(2\pi -\frac{\pi }{2})i}{r}$

Special cases

1. If the Distribution of current across the diameter then $B_0=0$

2. If Current between any two points on the circumference then $B_0=0$

3. Concentric co-planar circular loops carrying the same current in the Same Direction-

$B_{\text{centre }}=\frac{{\mu }_o}{4\pi }(2\pi i)[\frac{1}{r_1}+\frac{1}{r_2}]$

If the direction of currents are the same in concentric circles but have a different number of turns then
$B_{\text{centre }}=\frac{{\mu }_o}{4\pi }(2\pi i)[\frac{n_1}{r_1}+\frac{n_2}{r_2}]$

4. Concentric co-planar circular loops carrying the same current in the opposite Direction

$B_{\text{centre }}=\frac{{\mu }_o}{4\pi }(2\pi i)[\frac{1}{r_1}-\frac{1}{r_2}]$

If the number of turns is not the same i.e $n_1\ne n_2$
$B_{\text{centre }}=\frac{{\mu }_o}{4\pi }(2\pi i)[\frac{n_1}{r_1}-\frac{n_2}{r_2}]$

5. Concentric loops but their planes are perpendicular to each other

\text { Then } B_{\text {net }}=\sqrt{B_1^2+B_2{ }^2}

6. Concentric loops but their planes are at an angle ϴ with each other

$B_{net}=\sqrt{B_1{}^2+B_2{}^2+2B_1{B}_2\cos \theta }$

The Magnetic Field on the Axis of the Circular Current-Carrying Loop

In the below figure, it is shown that a circular loop of radius R carries a current $I$. Application of Biot-Savart law to a current element of length $dl$ at angular position $\theta$ with the axis of the coil.
the current in the segment $d\ell$ causes the field $d\overline{B}$ which lies in the $x$-y plane as shown below.

Another symetric $d{\ell }^{\prime }$ element that is diametrically opposite to previously $d\ell$ element cause $d\overrightarrow{B^{\prime }}$

Due to symmetry the components of $d\overrightarrow{B}$ and $d{\overrightarrow{B}}^{\prime }$ perpendicular to the $x$-axis cancel each other. i.e., these components add to zero.

The x -components of the $d\overrightarrow{B}$ combine to give the total field $\overrightarrow{B}$ at point P.

We can use the law of Biot-Savart to find the magnetic field at point P on the axis of the loop, which is at a distance x from the centre.

$d\overline{\ell }$ and $\hat{r}$ are perpendicular and the direction of field $d\overline{B}$ caused by this particular element $d\overline{\ell }$ lies in the $x$-y plane.

The magnetic field due to the current element is
$\mathrm{dB}=\frac{{\mu }_0\mathrm{I}}{4\pi }\int \frac{\mathrm{d}\mathbf{l}\times \hat{\mathbf{r}}}{{\mathrm{r}}^2}.$

Since $r^2=x^2+R^2$
the magnitude $dB$ of the field due to element $d\overline{\ell }$ is:
$dB=\frac{{\mu }_{0}I}{4\pi }\frac{d\ell }{(x^2+R^2)}$

The components of the vector $dB$ are
$\begin{array}{rl}& d{B}_x=dB\sin \theta =\frac{{\mu }_{0}I}{4\pi }\frac{d\ell }{(x^2+R^2)}\frac{R}{{(x^2+R^2)}^{1/2}}\dots (1)\\ & d{B}_y=dB\cos \theta =\frac{{\mu }_{0}I}{4\pi }\frac{d\ell }{(x^2+R^2)}\frac{x}{{(x^2+R^2)}^{1/2}}\dots (2)\end{array}$

$$\begin{array}{rl}& \text{ Total magnetic field along axis }=B_{\text{axis }}=\int d{B}_x=\int dB\sin \theta \\ & \because \int d{B}_y=\int dB\cos \theta =0\end{array}$$

Everything in this expression except $d\overrightarrow{\ell }$ is constant and can be taken outside the integral.
The integral $d\overrightarrow{\ell }$ of is just the circumference of the circle, i.e., $\int d\ell =2\pi R$
So, we get
$\Rightarrow B_{\text{axis }}=\frac{{\mu }_{0}I{R}^2}{2{(x^2+R^2)}^{3/2}}\text{ (on the axis of a circular loop) }$

• If x>>R, then $B=\frac{{\mu }_{0}I{R}^2}{2x^3}$.
• At centre , $x=0\Rightarrow B_{\text{centre }}=\frac{{\mu }_0}{4\pi }\cdot \frac{2\pi Ni}{R}=\frac{{\mu }_{0}Ni}{2R}=B_{max}$

Recommended Topic Video

Solved Examples Based on Biot-Savart Law

Example 1: The direction of current in a current element $I\overrightarrow{dl}$ is

1) As that of current in the wire

2) Opposite the direction of current in the wire

3) It's a scalar quantity

4) Always circular

Solution:

Current Element

It is the product of the current and length of the infinitesimal segment of the current wire.

wherein

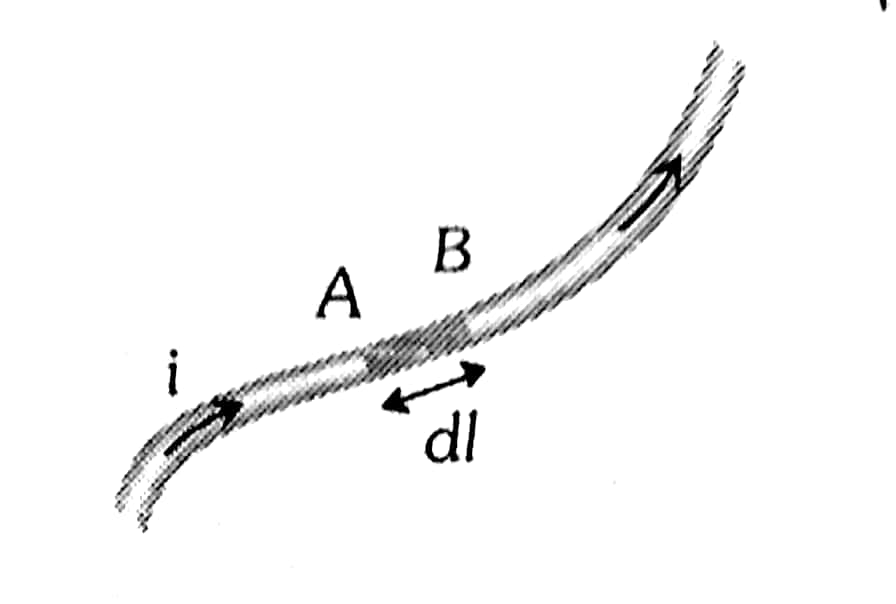
The current element is a vector quantity, and the direction is the same as the current in the wire.

Example 2: Unit (S.I.) of the current element $(I\overrightarrow{dl})$:

1) Ampere

2) Ampere metre

3) Newton

4) Tesla

Solution:

The current element $I\overrightarrow{dl}$ is taken as vea ctor quantity.
S.I. unit is $I\overrightarrow{dl}=$ Ampere meter.

Hence, the answer is option (2).

Example 3: A current I flow in an infinitely long wire cross-section in the form of a semicircular ring of radius R. The magnitude of the magnetic field induction along its axis is:

1) $\frac{\mu oI}{2{\pi }^{2}R}$
2) $\frac{\mu oI}{2\pi R}$
3) $\frac{\mu oI}{4\pi R}$
4) $\frac{\mu oI}{{\pi }^{2}R}$

Solution:

Magnetic field due to Current Element

$\overrightarrow{dB}=K\frac{idl\sin \mathrm{\Theta }}{r^2}\Rightarrow \overrightarrow{B}=\int \overrightarrow{dB}=\frac{{\mu }_0}{4\pi }\int \frac{dl\sin \mathrm{\Theta }}{r^2}$

$\begin{array}{rl}& dI=\frac{d\mathrm{\Theta }}{\pi }I\\ & dB=\frac{\mu o}{4\pi }\cdot \frac{2I}{R}=\frac{\mu oI}{2{\pi }^{2}R}d\mathrm{\Theta }\to \text{ M.Fat centre due to this portion }\end{array}$

Net magnetic field
$\begin{array}{rl}& B={\int }_{-\frac{\pi }{2}}^{+\frac{\pi }{2}}dB\cos \mathrm{\Theta }\to \\ & B={\int }_{-\frac{\pi }{2}}^{+\frac{\pi }{2}}\frac{\mu oI}{2{\pi }^{2}R}\cos \mathrm{\Theta }d\mathrm{\Theta }=\frac{\mu oI}{{\pi }^{2}R}\end{array}$

Example 4: A straight section PQ of a circuit lies along the X-axis from $x=-\frac{a}{2}$ to $x=\frac{a}{2}$ and carries a steady current $i$. The magnetic field due to the section $PQ$ at a point $X=+a$ will be:

1) Proportional to a
2) Proportional to $a^2$
3) Proportional to $\frac{1}{a}$
4) Zero

Solution:

Magnetic field due to Current Element

If $\mathrm{\Theta }=0^{\circ }$ or $\mathrm{\Theta }=\pi$
$\sin \mathrm{\Theta }=0$

wherein

Thus field at a point on the line of wire is zero.

The magnetic field at a point on the axis of a current-carrying wire is always zero.

Example 5: An arc of a circle of radius $R$ subtends an angle $\mathrm{\Theta }=\frac{\pi }{2}$ at the centre. It carries a current I. The magnetic field at the centre will be:

1) $\frac{\mu oI}{2R}$
2) $\frac{\mu oi}{8R}$
3) $\frac{\mu Oi}{4R}$
4) $\frac{2\mu oi}{5R}$

Solution:

$B=\frac{{\mu }_o}{4\pi }\times \frac{\mathrm{\Theta }i}{R}=\frac{{\mu }_o}{4\pi }\times \frac{\pi }{2}\times \frac{i}{R}\Rightarrow \frac{{\mu }_{o}i}{8R}$

Hence, the answer is option (2)