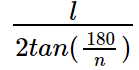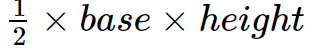Area Of Polygon - Definition & Finding Area of N Sided Polygons

Edited By Team Careers360 | Updated on Jul 02, 2025 05:19 PM IST

The surface that a polygon occupies is known as its area. There are both regular and irregular polygons. The fundamental polygons used in geometry include triangles, squares, rectangles, pentagons, and hexagons, among others. Each of these polygons has a different area. All measurements are taken in square units, which are the standard measuring unit.

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

This Story also Contains

What Is A Polygon?
Types Of Polygons
How To Find A Regular Polygon’s Area?
How To Determine An Irregular Polygon’s Area?
Formulas For Calculating Area Of Few Polygons
Points To Remember

What Is A Polygon?

In mathematics, a polygon is a structure made of adjacent straight lines and is a part of geometry. Several straight lines come together to create a polygonal chain or circuit. Another way to describe it is as a rigid plane that is connected by two or more circuits. There are both regular and irregular polygons.

Types Of Polygons

A polygon can be categorised as regular or irregular based on the length of its sides.

Regular polygon - Any polygon with equal sides and angles is said to be regular.
Irregular polygon - A closed plane shape with unequal sides and angles is known as an irregular polygon.

How To Find A Regular Polygon’s Area?

If the number of sides of a regular polygon is known, one may use the formula to calculate its area,

Area of polygon is computed as: (Length of one side * Number of sides * Apothem)/2

Here, the apothem's length is indicated as:

Length of apothem = \frac{l}{2tan(\frac{180}{n})} 1706510693133

Here, the regular polygon has a side length of “l” and a number of sides, “n”.

The area of a regular polygon is expressed in terms of its perimeter as follows:

Area of polygon = (Perimeter * apothem)/2, where the perimeter of the polygon = Number of sides * Length of one side.

How To Determine An Irregular Polygon’s Area?

We divide an irregular polygon into a collection of regular polygons whose areas can be calculated using existing methods. This allows us to determine the area of irregular polygons.

Formulas For Calculating Area Of Few Polygons

Triangle - \frac{1}{2}\times base\times height

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Heron's formula can be used to determine a triangle's area if we know the length of its sides, that is, Area = \sqrt{s(s-a)(s-b)(s-c)} 1706510692794

Square - (side)^{2}
Rectangle - Length x Breadth
Pentagon - 5/2 × side length × distance from the center of sides to the center of pentagon
Rhombus - 1/2 × product of diagonals
Hexagon - (3√3)/2 × distance from center of sides to the center of hexagon
Parallelogram - Base * Height
Trapezium - (1/2) × (sum of lengths of its parallel sides or bases) × height

Points To Remember

Finding an apothem allows one to determine the area of a regular polygon given the length of one side.
Apothem divides a side into two equal portions by falling on its midway at a right angle.
While a square has four sides, an equilateral triangle has three, making it a regular polygon. They are therefore not prefixed as regular before the form name.

Frequently Asked Questions (FAQs)

1. What is a polygon?

In mathematics, a polygon is a structure made of adjacent straight lines and is a part of geometry.

2. Name the two types of polygons.

Based on the length of its sides, a polygon can be classified as:

Regular polygon
Irregular polygon

3. How to find the area of a regular polygon?

If the number of sides of a regular polygon is known, one may use the formula to calculate its area,

Area of polygon is calculated as: (Number of sides * Length of one side * Apothem)/2

4. Define irregular polygons

A closed plane shape with unequal sides and angles is known as an irregular polygon.

5. What is the significance of the number of sides (n) in calculating the area of a regular polygon?

The number of sides (n) in a regular polygon is crucial because it determines the polygon's internal angles and the relationship between its side length and radius. As n increases, the polygon more closely approximates a circle, which affects how we approach area calculation.

6. What is the importance of the apothem in calculating the area of a regular polygon?

The apothem is the perpendicular distance from the center of a regular polygon to any of its sides. It's crucial in area calculations because the area of a regular polygon can be expressed as (1/2) × perimeter × apothem. This formula essentially divides the polygon into triangles, each with base (side length) and height (apothem).

7. What is the significance of Green's Theorem in calculating the area of complex polygons?

Green's Theorem relates a line integral around a simple closed curve to a double integral over the plane region bounded by the curve. For polygons, this means we can calculate the area by integrating around the boundary instead of over the entire region, which can be simpler for complex shapes.

8. What role does the cross product play in calculating the area of a polygon in three-dimensional space?

In 3D space, the cross product of two vectors representing sides of a polygon gives a vector whose magnitude is twice the area of the parallelogram formed by these sides. This principle can be extended to find the area of any polygon in 3D space by breaking it into triangles and summing their areas.

9. How does the concept of signed area apply to polygons, and why is it important?

Signed area takes into account the orientation of the polygon's boundary. When calculating area using line integrals or cross products, the result can be positive or negative depending on the direction of integration. Understanding signed area is crucial for correctly handling complex or self-intersecting polygons.

10. How does the area formula for a regular polygon change as the number of sides increases?

As the number of sides (n) in a regular polygon increases, the formula for its area approaches that of a circle. The general formula for a regular polygon's area is (1/4)n(s^2)cot(π/n), where s is the side length. As n approaches infinity, this formula converges to πr^2, the area of a circle.

11. What is the fundamental principle behind using integrals to find the area of a polygon?

The fundamental principle is to break down the polygon into infinitesimally small vertical strips. The area of each strip is approximately a rectangle, with width dx and height f(x). By integrating these strips over the entire width of the polygon, we sum up all these tiny areas to get the total area.

12. What is the relationship between a polygon's perimeter and its area?

While there's no direct formula relating a polygon's perimeter to its area for all polygons, there is a relationship. Generally, among polygons with the same perimeter, those with more sides tend to have larger areas. This relationship is captured in the isoperimetric inequality, which states that the circle has the largest area for a given perimeter.

13. How can we use the concept of limits to understand the area of polygons with many sides?

As we increase the number of sides in a regular polygon, its shape approaches that of a circle. By taking the limit of the polygon's area formula as n (number of sides) approaches infinity, we can derive the formula for the area of a circle. This concept illustrates the connection between polygons and circles in calculus.

14. How does the concept of area for polygons relate to integrals?

The area of a polygon can be calculated using integrals when the polygon is defined by a function or set of functions. This approach is especially useful for irregular or complex polygons. The integral allows us to sum up infinitesimal areas along the shape, giving us the total area.

15. What is the relationship between the area of a polygon and the sum of its interior angles?

For any polygon with n sides, the sum of its interior angles is (n-2) × 180°. While this doesn't directly give us the area, it's related to the polygon's shape and thus indirectly to its area. As n increases, both the sum of interior angles and the area increase, approaching the properties of a circle.

16. How does the method for finding the area of a polygon differ for regular and irregular polygons?

For regular polygons, we can often use simple formulas based on the number of sides and side length. For irregular polygons, we typically need to use more advanced techniques like integration or breaking the shape into simpler parts. Integrals are particularly useful for irregular polygons defined by functions.

17. How does the concept of winding number relate to calculating the area of self-intersecting polygons?

The winding number describes how many times a polygon's boundary wraps around a point. For self-intersecting polygons, different regions may have different winding numbers. By considering these winding numbers, we can correctly calculate the signed area of complex, self-intersecting polygons.

18. What is the significance of Pick's theorem in calculating the area of lattice polygons?

Pick's theorem provides a simple way to calculate the area of a polygon whose vertices all lie on lattice points (integer coordinates). The formula is A = i + b/2 - 1, where i is the number of lattice points inside the polygon and b is the number on the boundary. This theorem connects discrete geometry with continuous area.

19. How does the method of exhaustion relate to finding the area of polygons with curved boundaries?

The method of exhaustion, an ancient precursor to integral calculus, involves approximating the area of a shape with curved boundaries by using inscribed or circumscribed polygons. As the number of sides of these polygons increases, their areas converge to the area of the curved shape. This concept is fundamental to understanding how integration calculates areas.

20. What is a polygon in the context of area calculation?

A polygon is a closed, two-dimensional shape with straight sides. In the context of area calculation, we focus on the region enclosed by these sides. Polygons can have any number of sides, from triangles (3 sides) to shapes with many more sides.

21. How does the concept of fractal dimension relate to the areas of certain types of polygons?

Fractal dimension describes how the "size" of a shape changes with scale. Some polygons, like Koch snowflakes, have fractal boundaries. While these polygons have finite areas, their perimeters can be infinite. Understanding fractal dimension helps us analyze such unusual polygons and their properties.

22. How does the concept of homology relate to calculating areas of polygons with holes?

Homology theory provides a framework for understanding the topology of shapes, including polygons with holes. In the context of area calculation, it helps us correctly account for holes in a polygon. The first homology group, for instance, can tell us about the number of holes, which affects how we approach area calculation.

23. What is the relationship between the area of a polygon and its circumscribed and inscribed circles?

For a regular polygon, the area is always less than that of its circumscribed circle and greater than that of its inscribed circle. As the number of sides increases, these three areas converge. This relationship provides bounds for the polygon's area and illustrates the connection between polygons and circles.

24. What is the significance of the Gauss-Bonnet theorem in relation to polygon areas?

The Gauss-Bonnet theorem relates the geometry of a surface (its curvature) to its topology (its Euler characteristic). For polygons on curved surfaces, this theorem provides a way to relate the sum of the polygon's interior angles to its area and the curvature of the surface it's on, generalizing the flat-space relationship.

25. How does integration help in finding the area of an irregular polygon?

Integration helps find the area of an irregular polygon by summing up infinitesimal areas. If we can express the boundary of the polygon as a function y = f(x), we can integrate f(x) over the appropriate interval to find the area. For more complex shapes, we might need to use multiple integrals or break the shape into parts.

26. How does the method of triangulation apply to finding the area of irregular polygons?

Triangulation involves dividing an irregular polygon into triangles. By calculating the areas of these individual triangles and summing them up, we can find the total area of the polygon. This method is particularly useful when the polygon is defined by its vertices rather than by a function.

27. How does the concept of symplectic area relate to polygon areas in phase space?

Symplectic area is a generalization of area to phase space in classical mechanics. For polygons in phase space (where each point represents both position and momentum), the symplectic area is preserved under certain transformations. This concept is crucial in understanding area-preserving maps and their applications in physics and mathematics.

28. What is the significance of the isoperimetric quotient in analyzing polygon areas?

The isoperimetric quotient is the ratio of a polygon's area to the area of a circle with the same perimeter. It's always less than or equal to 1, with equality only for circles. This quotient helps us understand how "efficient" a polygon is in enclosing area for a given perimeter, providing insights into optimal shapes and efficiency in various applications.

29. How does the method of finite elements relate to calculating areas of complex polygons?

The finite element method involves dividing a complex shape into smaller, simpler elements (often triangles or quadrilaterals). For polygons, this method can be used to approximate areas of very complex or irregular shapes by summing the areas of these smaller elements. It's particularly useful in numerical analysis and engineering applications.

30. What is the shoelace formula, and how is it used to calculate polygon areas?

The shoelace formula (also known as the surveyor's formula) is a method for calculating the area of a polygon based on its vertex coordinates. It involves taking the sum of the products of x-coordinates and adjacent y-coordinates in a cyclic manner. This method is particularly useful for polygons defined by their vertex coordinates.

31. How does the concept of moment of inertia relate to the area of a polygon?

The moment of inertia of a polygon is related to how its area is distributed around an axis. While not directly giving the area, moments can be used to calculate areas of complex shapes. The second moment of area, for instance, is used in calculating the area of polygons in some advanced applications.

32. What is the role of the centroid in calculating the area of a polygon?

The centroid is the geometric center of a polygon. While not directly used in area calculation, the centroid's coordinates can be found using area integrals. Conversely, if we know the centroid and can divide the polygon into simpler shapes, we can use this information to help calculate the total area.

33. How does the concept of differential forms apply to calculating polygon areas in higher dimensions?

Differential forms provide a coordinate-independent approach to integration. In the context of polygon areas, they allow us to generalize the concept of area to higher dimensions and more complex geometries. This approach is particularly useful for calculating areas of polygons on curved surfaces or in non-Euclidean geometries.

34. What is the significance of the divergence theorem in relation to polygon areas?

The divergence theorem, which relates the flux of a vector field through a closed surface to the divergence of the field within the volume, can be applied to polygons in 2D. It provides an alternative way to calculate areas by relating the boundary integral to an integral over the interior, which can be useful for complex shapes.

35. How does the concept of conformal mapping apply to calculating areas of polygons?

Conformal mapping preserves angles but not necessarily areas. However, we can use conformal maps to transform complex polygons into simpler shapes whose areas are easier to calculate. By understanding how the mapping affects areas, we can then relate the area of the transformed shape back to the original polygon.

36. What is the role of complex analysis in calculating areas of certain polygons?

Complex analysis provides powerful tools for area calculation, especially for polygons with vertices defined in the complex plane. Techniques like contour integration and the residue theorem can be used to calculate areas of complex polygons, often providing elegant solutions to otherwise difficult problems.

37. What is the role of Stokes' theorem in calculating areas of polygons on curved surfaces?

Stokes' theorem generalizes the fundamental theorem of calculus to higher dimensions. For polygons on curved surfaces, it allows us to relate a surface integral (area) to a line integral around the boundary. This is particularly useful for calculating areas of polygons on non-flat surfaces, where traditional methods may not apply.

38. How does the concept of differential geometry apply to calculating areas of polygons on curved surfaces?

Differential geometry provides tools to understand the intrinsic properties of surfaces. For polygons on curved surfaces, we need to consider the metric of the surface to correctly calculate areas. Concepts like the first fundamental form allow us to compute areas by integrating over the polygon while accounting for the surface's curvature.

39. What is the significance of the Euler characteristic in relation to polygon areas?

The Euler characteristic (χ = V - E + F, where V, E, and F are the numbers of vertices, edges, and faces) is a topological invariant. While not directly related to area, it provides information about the structure of a polygon or polyhedron. For polygons with holes, understanding the Euler characteristic is crucial for correctly approaching area calculations.

40. How does the concept of measure theory extend our understanding of polygon areas?

Measure theory provides a rigorous foundation for the concept of area (and volume in higher dimensions). It allows us to define area for a much broader class of sets than just polygons. This theory is crucial for understanding area in more abstract settings and for dealing with pathological cases that might arise in advanced mathematics.

41. What is the role of algebraic geometry in analyzing areas of certain types of polygons?

Algebraic geometry studies geometric objects defined by polynomial equations. For polygons whose boundaries are defined by algebraic curves, techniques from algebraic geometry can be powerful tools for area calculation. This approach is particularly useful for analyzing properties of areas of families of polygons defined by parametric equations.

42. How does the concept of tropical geometry relate to polygon areas?

Tropical geometry is a relatively new field that replaces the usual arithmetic operations with min and max operations. In the context of polygons, tropical geometry provides new ways to think about areas, especially for polygons defined in tropical space. This can lead to simplified calculations and new insights in certain types of optimization problems.

43. What is the significance of the Minkowski sum in relation to polygon areas?

The Minkowski sum is an operation that combines two sets of points by adding each point from one set to each point from the other. For polygons, the Minkowski sum creates a new polygon. Understanding how the areas of the original polygons relate to the area of their Minkowski sum is important in fields like computer graphics and robotics.

44. How does the concept of information theory relate to optimal representations of polygon areas?

Information theory deals with the quantification, storage, and communication of information. In the context of polygon areas, it can help us understand the most efficient ways to represent and communicate the shape and area of a polygon. This is particularly relevant in data compression and computer graphics applications.

45. What is the role of spectral theory in analyzing properties of polygon areas?

Spectral theory studies the properties of operators, particularly their eigenvalues and eigenfunctions. For polygons, spectral methods can be used to analyze properties of the Laplacian operator defined on the polygon. This can provide insights into the polygon's area and other geometric properties, especially for drumhead-like problems in mathematical physics.

46. How does the concept of optimal transport relate to comparing areas of different polygons?

Optimal transport theory deals with the problem of moving mass from one distribution to another in the most efficient way. In the context of polygons, it can be used to compare areas of different polygons by finding the most efficient way to "morph" one polygon into another. This provides a metric on the space of polygons that takes into account both shape and area.

47. What is the significance of the Brunn-Minkowski inequality in relation to polygon areas?

The Brunn-Minkowski inequality relates the volumes (or areas in 2D) of two sets and their Minkowski sum. For polygons, it states that the nth root of the area of the Minkowski sum of two polygons is greater than or equal to the sum of the nth roots of their individual areas. This inequality provides important insights into the behavior of polygon areas under various operations.

48. How does the concept of persistent homology apply to analyzing areas of families of polygons?

Persistent homology is a method from topological data analysis that tracks how topological features persist as a parameter changes. For families of polygons, it can be used to analyze how areas and other geometric properties change as the polygons are deformed or as parameters defining the polygons vary. This provides a robust way to study the stability of area calculations.

49. What is the role of category theory in providing a unified framework for understanding polygon areas?

Category theory provides a language for describing mathematical structures and their relationships. In the context of polygon areas, it can help unify different approaches to area calculation (e.g., geometric, algebraic, analytic) by