Angles – Definition, Parts, Types, FAQs, Examples

We can define an angle as the figure formed when the two lines or the rays converge at a common point, and we measure the angle formed at their point of meeting. In this article, we will learn about angles and their related concepts in detail. We will cover concepts like Angle definition in maths, critical angle definition, adjacent angle definition, right angle definition and example, and much more.

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

This Story also Contains

1. Angle Definition in Maths
2. Types of Angles
3. Angle Examples

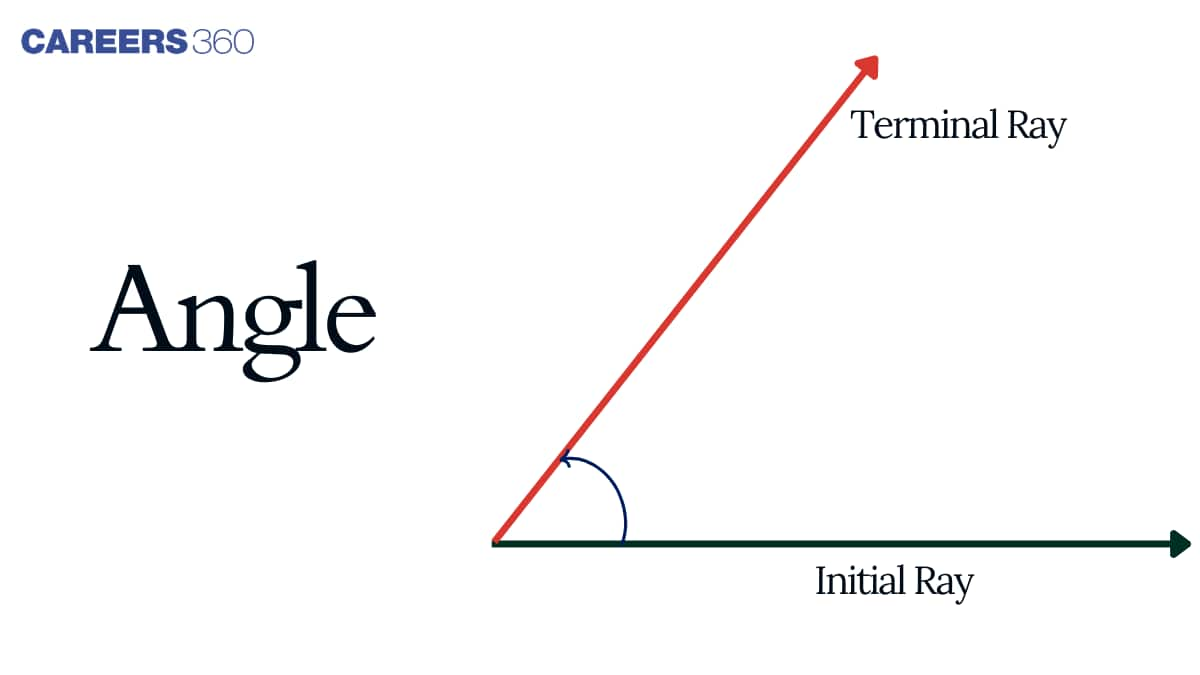
Angle Definition in Maths

The word “angle” is derived from the Latin word “angulus”, which means “corner”. When two rays come to meet at a point, we say that an angle is formed. Those two rays are called the sides of an angle, and the common endpoint is called the vertex, can be denoted using the Greek letter θ, α, β etc.

Positive Angle: If the path of angle is in counterclockwise direction, then we say it is positive angle.

Negative Angle: If the path of angle is in clockwise direction, then we say it is negative angle.

How do we Label Angles?

Method 1: In this method, we try to give a name to the angle like "p", "y", etc or by using Greek Letters for example alpha ( $\alpha )$, beta $(\beta )$, theta $(\theta )$, etc.

Method 2: We can also name them by using three letters on the shapes. We should remember that the middle letter should be the vertex always(the meeting point of the two rays).

For example, XYZ is a triangle. To represent the angle Y equal to 40 degrees, we define it as $\mathrm{\angle }ZYX={40}^{\circ }$

Parts of an Angle

We can say that an angle has various parts such as: Arms, Vertex, Initial Side and Terminal Side. We will discuss them one by one.

In the above diagram, we can see that at the vertex O the two arms of the angle namely PO and QO meet. Now we define the above terms individually,

1. Arms: These are the two long rays that meet at a particular point. In this example the arms are PO and OQ.

2. Vertex: It is the common point of the meeting of arms. O is the vertex here.

3. Initial side: It is the starting position of a ray that is rotated to form an angle.

4.Terminal side: It is the ending position of a ray that is rotated to form an angle.

How do we Measure the Angle?

We usually use the degrees $\left({}^{\circ }\right)$ measure for the representation of angles. We may measure the angles with the help of a "protractor". It has two sets of numbers going in opposite directions, one set from 0 to 180 degree on the outer rim and the other from 180 to 0 degree on the inner rim.

To measure the angle using a protractor, place the straight line of the protractor on one arm of the angle and note the angle measurement where the second arm touches the protractor.

Types of Angles

Here we define various types of angles:

Acute Angle definition – These always measure less than 90 degrees.

Right Angle definition and example – They are exactly 90 degrees. For example when the clock strikes 9 am.

Obtuse Angle definition – The measure lies between the range of 90 to 180 degrees.

Straight Angle definition – Angle which is exactly 180 degrees.

Reflex Angle definition – The range is between 180 to 360 degrees.

Complete Angle definition – The angle that measures exactly at 360 degrees.

Complementary Angle definition - The 2 angles who sum up to give 90 degrees.

Critical Angle definition - Its measure is also 90 degrees and used in physics in the topic of reflection and optics.

Zero angle definition - It measures 0 degrees and represents no rotation. It is formed when 2 rays overlap each other.

Vertically opposite angle definition - The angles that lie opposite to each other when 2 lines intersect one another.

Adjacent angle definition - They always are placed next to one another.

Acceptance angle definition - They are used in optics in physics.

Exterior angle definition - Angle that is formed between any side of a shape and a line extended to one side.

Interior angle definition - The angle that is formed within a figure.

Supplementary angle definition - The 2 angles who sum up to 180 degrees.

We can also classify them as complementary angles, supplementary angles, adjacent angles, etc.

Here we list some significant theorems based on lines and angles.

When two parallel lines are cut by a transversal, following properties hold :

• Alternate interior angles, alternate exterior angles and corresponding angles are of same measure.
• Interior angles on the same side of the transversal are always supplementary.
• Vertical angles are congruent when the straight line intersects the lines. The lines may be either parallel or not-parallel.
• The sum of all angles on one side of a straight line is always equal to 180 degrees.
• Around a point, sum of all angles is always equal to 360 degrees.

Angle Examples

Example 1: Find the unknown angle $p$ for the given triangle $PQR$, where $\mathrm{\angle }P={38}^{\circ }$ and $\mathrm{\angle }Q={95}^{\circ }$

Solution: Given that $\mathrm{\angle }P={38}^{\circ }$ and $\mathrm{\angle }Q={95}^{\circ }$
Let $\mathrm{\angle }R=p$
We know that the sum of interior angles of a triangle is ${180}^{\circ }$. Hence,

$\begin{array}{rl}& \mathrm{\angle }\mathrm{P}+\mathrm{\angle }\mathrm{Q}+\mathrm{\angle }\mathrm{R}={180}^{\circ }\\ & {38}^{\circ }+{95}^{\circ }+\mathrm{p}={180}^{\circ }\\ & {133}^{\circ }+p={180}^{\circ }\\ & p={180}^{\circ }-{133}^{\circ }\\ & p={47}^{\circ }\end{array}$

Example 2: Find the unknown angle in a quadrilateral $PQRS$, where $\mathrm{\angle }P={100}^{\circ },\mathrm{\angle }Q=$ ${50}^{\circ },\mathrm{\angle }R={40}^{\circ }$. Find the unknown angle $S$.

Solution: $\mathrm{\angle }P={100}^{\circ },\mathrm{\angle }Q={50}^{\circ },\mathrm{\angle }R={40}^{\circ }$

$\begin{array}{rl}& \mathrm{\angle }\mathrm{P}+\mathrm{\angle }\mathrm{Q}+\mathrm{\angle }\mathrm{R}+\mathrm{\angle }\mathrm{S}={360}^{\circ }\dots ..(1)\text{ (angle sum property of quadrilateral) }\\ & {100}^{\circ }+{50}^{\circ }+{40}^{\circ }+\mathrm{\angle }\mathrm{S}={360}^{\circ }\\ & {190}^{\circ }+\mathrm{\angle }\mathrm{S}={360}^{\circ }\\ & \mathrm{\angle }\mathrm{S}={360}^{\circ }-{190}^{\circ }\\ & \mathrm{\angle }\mathrm{S}={170}^{\circ }\end{array}$

Example 3: Classify the following angles into acute angles, obtuse angles, right angles, or reflex angles.
a) ${22}^{\circ }$
b) ${155}^{\circ }$
c) ${90}^{\circ }$
d) ${70}^{\circ }$

Solution:
(a) ${22}^{\circ }$ lies in between $0^{\circ }$ and ${90}^{\circ }$, so it is an acute angle.
(b) ${155}^{\circ }$ lie between the range of ${90}^{\circ }$ and ${180}^{\circ }$, so it is an obtuse angle.
(c) ${90}^{\circ }$ right angle.
(d) ${70}^{\circ }$ is acute angle.

Example 4: Write true or false for the following statements:
a.) ${180}^{\circ }<$ Reflex angle $<{360}^{\circ }$
b.) $0^{\circ }<$ acute angle $<{90}^{\circ }$.

Solution:
a.) True since the range of reflex angles is from 180 to 360 degrees.
b.) True as $0^{\circ }<$ Acute angle $<{90}^{\circ }$

Example 5 : Identify the type of angle. (replace 40 by 50,117 by 116,121 by 120,185 by 160 ).

Solution:

a) Angle of measure ${50}^{\circ }$ is an acute angle.
b) The given angle is equal to ${116}^{\circ }$. It is an obtuse angle because its measure is greater than ${90}^{\circ }$ but less than ${180}^{\circ }$.
c) Angle of measure ${120}^{\circ }$ is an obtuse angle.
d) Angle of measure ${160}^{\circ }$ is an obtuse angle.

List of Topics Related to Angle Definition